Doğal Sayıyı Kesre Bölme
Kazanım: Bir doğal sayıyı bir kesre ve bir kesri bir doğal sayıya böler, bu işlemi anlamlandırır.
Bu konuda neler öğreneceğiz :
Doğal Sayıyı Kesre Bölme
Bir doğal sayının içinde kaç tane birim kesir olduğunu bulmak için doğal sayıyı birim kesre böleriz.
Örneğin; 6 doğal sayısının içinde kaç tane \dfrac{1}{3} birim kesri vardır bulalım.
➡️ 6 doğal sayısını göstermek için aşağıdaki gibi 6 tane dikdörtgen çizelim.
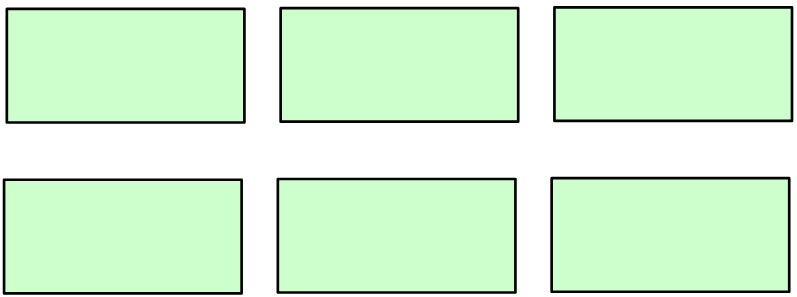
➡️ 6 doğal sayısının içinde kaç tane \dfrac{1}{3} olduğunu bulmak için dikdörtgenleri 3’e bölüp kaç tane birim olduğunu sayalım.
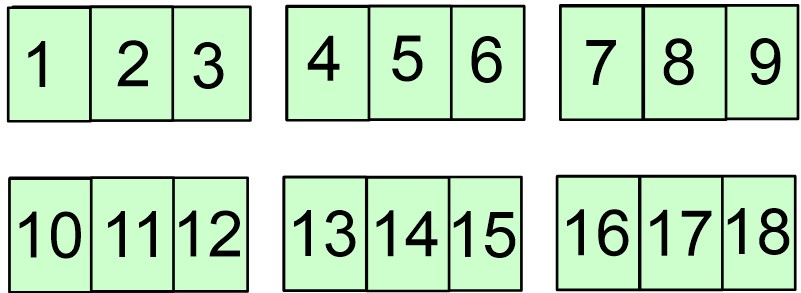
Yukarıdaki görselde görüldüğü gibi 6 doğal sayısının içinde 18 tane \dfrac{1}{3} vardır.
Bu yaptığımız işlem 6 doğal sayısını \dfrac{1}{3} kesrine bölme işlemidir.
O zaman 6÷ \dfrac{1}{3} = 18 olur.
Bilgi: Bir doğal sayıyı birim kesre bölerken doğal sayıyı aynen yazılır, kesirli sayı ise ters çevirip çarpılır.
Örneğin; 9 ÷ \dfrac{1}{4} bölme işlemini yapalım.
➡️ Doğal sayıyı aynen yazıp, kesirli sayıyı ters çevirip çarparız.
9 × \dfrac{4}{1}
\dfrac{9}{1} × \dfrac{4}{1}
\dfrac{36}{1}
36
Bilgi: Bir doğal sayıyı birim kesre bölerken ikinci bir yöntem olarak doğal sayı ile kesrin paydasını eşitleriz. Sonra payı, paya böleriz. Paydayı, paydaya böleriz.
Örneğin; 4 ÷ \dfrac{1}{5} bölme işlemini yapalım.
➡️ Doğal sayı ile kesrin paydasını eşitleyelim.
4 ÷ \dfrac{1}{5}
\dfrac{4}{1} ÷ \dfrac{1}{5}
🤓 Paydaları eşitleyelim.
\dfrac{4×5}{1×5} ÷ \dfrac{1}{5}
\dfrac{20}{5} ÷ \dfrac{1}{5}
➡️ Paydayı eşitledikten sonra pay ile payı, payda ile paydayı böleriz.
\dfrac{20÷1}{5÷5}
\dfrac{20}{1} = 20
Bir Doğal Sayıyı Bir Kesre Bölme
6’nın içinde kaç tane \dfrac{2}{3} olduğunu bulmak için 6 tane dikdörtgeni 3 parçaya ayıralım bu parçaların içinde kaç tane 2 adet parça olduğunu bulalım.
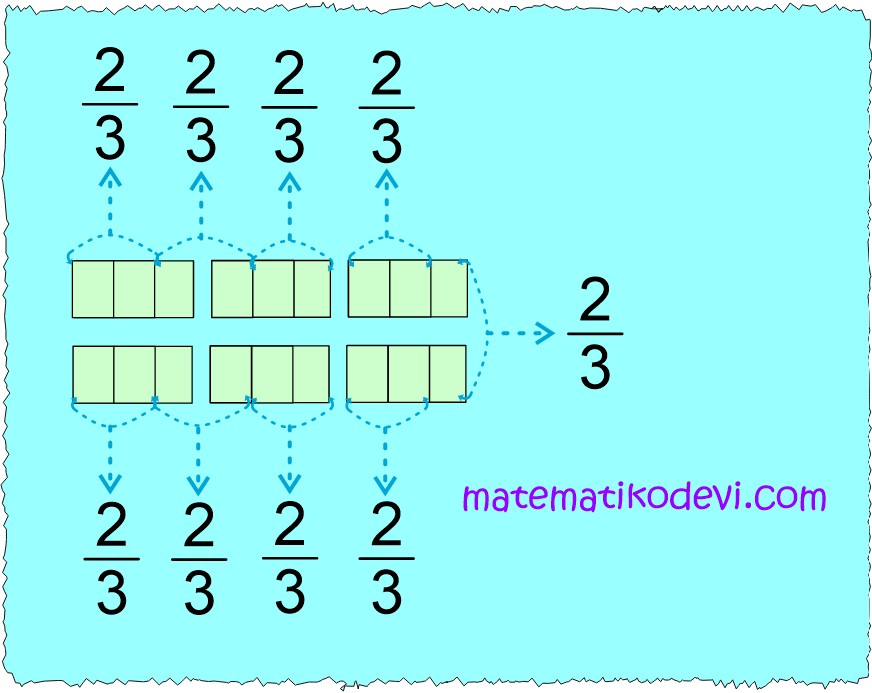
Yukarıda görseli incelediğimizde 6 tane dikdörtgenin içinde 9 tane \dfrac{2}{3} vardır.
Yaptığımız işlem bölme işlemidir. 👉 6 ÷ \dfrac{2}{3}
Bu bölme işleminin sonucunu yukarıdaki görselde görüldüğü gibi 9 olarak bulduk.
Yani 6 ÷ \dfrac{2}{3} = 9 olarak yazarız.
Bilgi: Bir doğal sayıyı bir kesre bölerken doğal sayı aynen yazılır, kesirli sayı ise ters çevirip çarpılır.
Örneğin; 12 ÷ \dfrac{6}{5} bölme işlemini yapalım.
➡️ Doğal sayıyı aynen yazıp, kesirli sayıyı ters çevirip çarparız.
12 × \dfrac{5}{6}
\dfrac{12}{1} × \dfrac{5}{6}
\dfrac{12×5}{1×6}
\dfrac{60}{6}
10
Örnek: 20 ÷ \dfrac{3}{4} bölme işlemini yapalım.
➡️ Doğal sayıyı aynen yazıp, kesirli sayıyı ters çevirip çarparız.
20 × \dfrac{4}{3}
\dfrac{20}{1} × \dfrac{4}{3}
\dfrac{20×4}{1×3}
\dfrac{80}{3}
Bir Kesri Doğal Sayıya Bölme
Bilgi: Bir kesri bir doğal sayıya bölerken kesri aynen yazarız, doğal sayıyı ise ters çevirip çarparız.
Örneğin; \dfrac{5}{4} ÷ 3 bölme işlemini yapalım.
➡️ Kesri aynen yazıp, doğal sayıyı ters çevirip çarparız.
3 doğal sayısının ters çevrilmiş hali \dfrac{1}{3} olur.
\dfrac{5}{4} × \dfrac{1}{3}
\dfrac{5×1}{4×3}
\dfrac{5}{12}
\dfrac{5}{4} ÷ 3 bölme işleminin sonucu \dfrac{5}{12} olur.
Örnek: \dfrac{6}{7} ÷ 4 bölme işlemini yapalım.
➡️ Kesri aynen yazıp, doğal sayıyı ters çevirip çarparız.
4 doğal sayısının ters çevrilmiş hali \dfrac{1}{4} olur.
\dfrac{6}{7} × \dfrac{1}{4}
\dfrac{6×1}{7×4}
\dfrac{6}{28}
\dfrac{6}{7} ÷ 4 bölme işleminin sonucu \dfrac{6}{28} olur.
Bilgi: Bölme işlemi yaparken tam sayılı kesir olursa, tam sayılı kesri bileşik kesre çevirip sonra bölme işlemini yaparız.
Tam sayılı kesri Bileşik kesre çevirme yöntemi için tıklayınız.
Örneğin; 2 \dfrac{1}{3} ÷ 4 bölme işlemini yapalım.
➡️ Tam sayılı kesri bileşik kesre çeviririz.
2 \dfrac{1}{3} = \dfrac{7}{3}
➡️ Bileşik kesre çevirdikten sonra bölme işlemini yaparız. (Kesri aynen yazıp, doğal sayıyı ters çevirip çarparız.)
4 doğal sayısının ters çevrilmiş hali \dfrac{1}{4} olur.
\dfrac{7}{3} × \dfrac{1}{4}
\dfrac{7×1}{3×4}
\dfrac{7}{12}
2 \dfrac{1}{3} ÷ 4 bölme işleminin sonucu \dfrac{7}{12} olur.
Sıra Sende 👉Aşağıdaki bölme işlemlerinin sonucunu bulunuz.
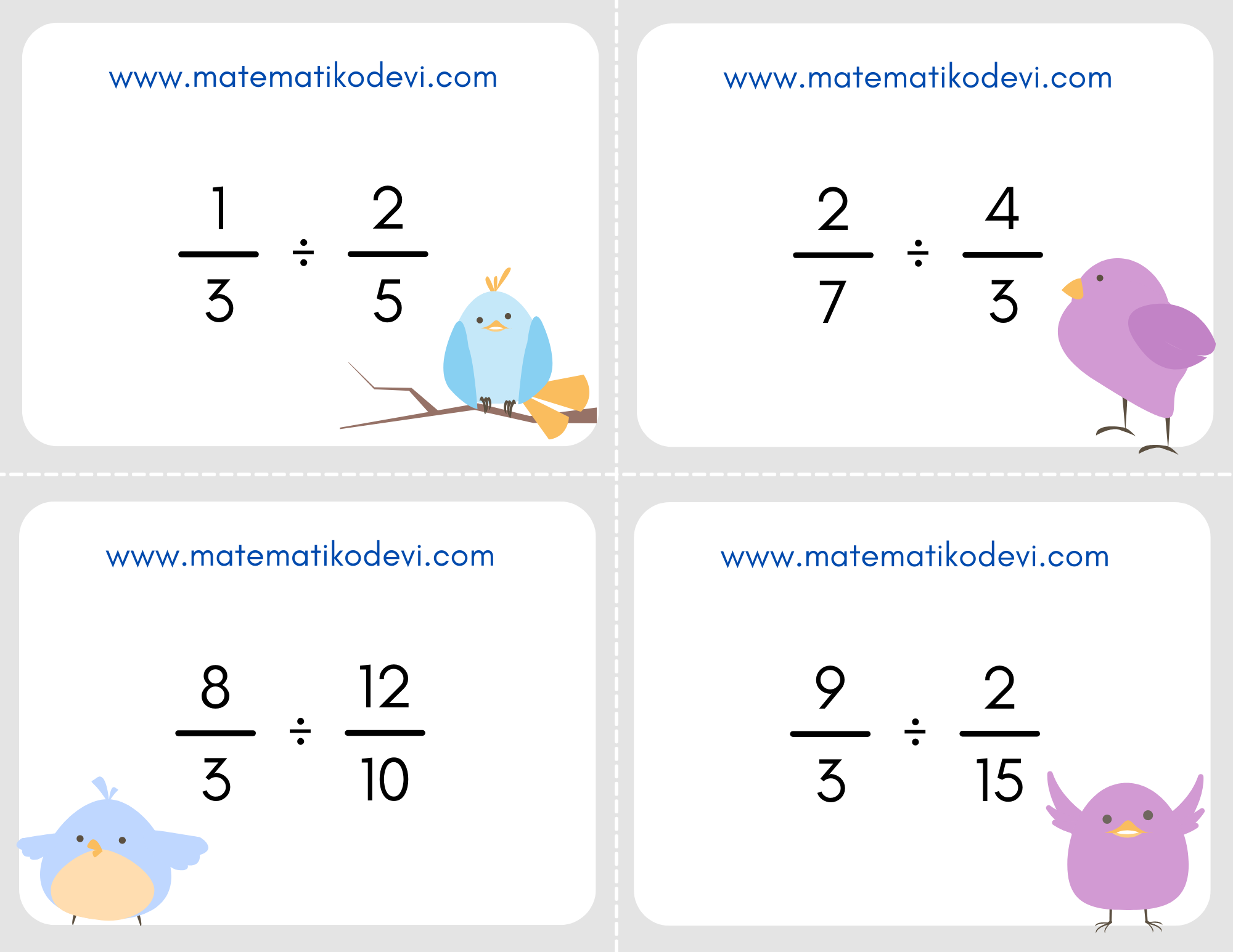
Cevaplar👇
\dfrac{1}{3} ÷ \dfrac{2}{5} = \dfrac{5}{6}
\dfrac{2}{7} ÷ \dfrac{4}{3} = \dfrac{3}{14}
\dfrac{8}{3} ÷ \dfrac{12}{10} = \dfrac{20}{9}
\dfrac{9}{3} ÷ \dfrac{2}{15} = \dfrac{45}{2}
🔻 Diğer konulara hızlı geçiş 🚀
| ⏪ Önceki Konu | Sonraki Konu ⏩ |
| Kesirlerde Çarpma İşlemi | Kesirlerde Bölme İşlemi |

