Tam Sayılı ve Bileşik Kesirler
Kazanım: Tam sayılı kesrin, bir doğal sayı ile bir basit kesrin toplamı olduğunu anlar ve tam sayılı kesri bileşik kesre, bileşik kesri tam sayılı kesre dönüştürür.
Bu konuda neler öğreneceğiz :
Tam Sayılı ve Bileşik Kesirler
Payı paydasından küçük olan kesirlere basit kesir, Payı paydasından büyük olan kesirlere tam bileşik kesir denir. Bileşik kesirler payı paydasından büyük olduğu için en az 1 bütünden oluşmaktadır. Bu durumda bileşik kesirleri doğal sayının ve basit kesrin toplamı şeklinde yazabiliriz. Bu şekilde yazdığımız kesirlere tam sayılı kesir denir.
z
Basit Kesirlere Örnekler:
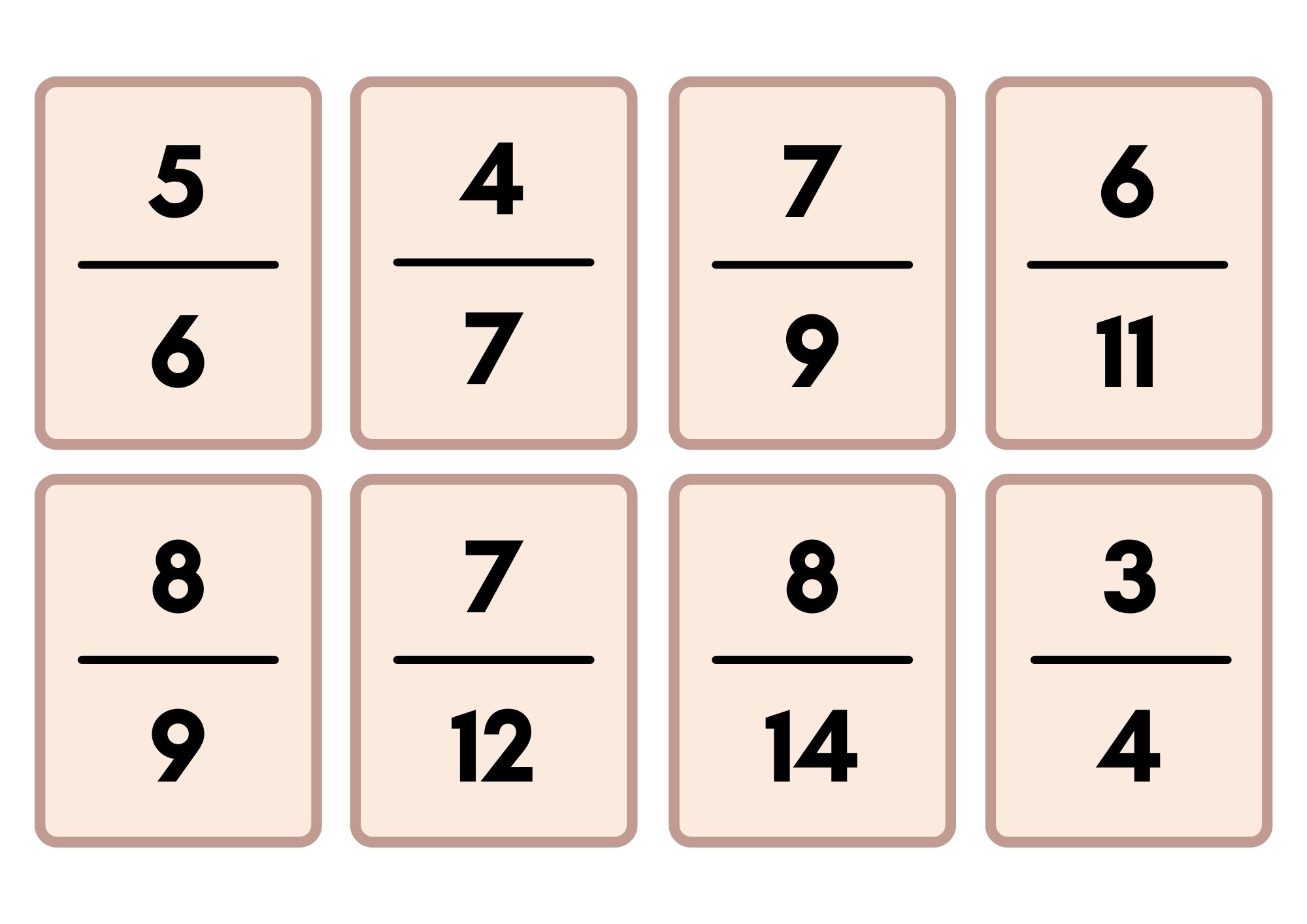
Bileşik Kesirlere Örnekler:
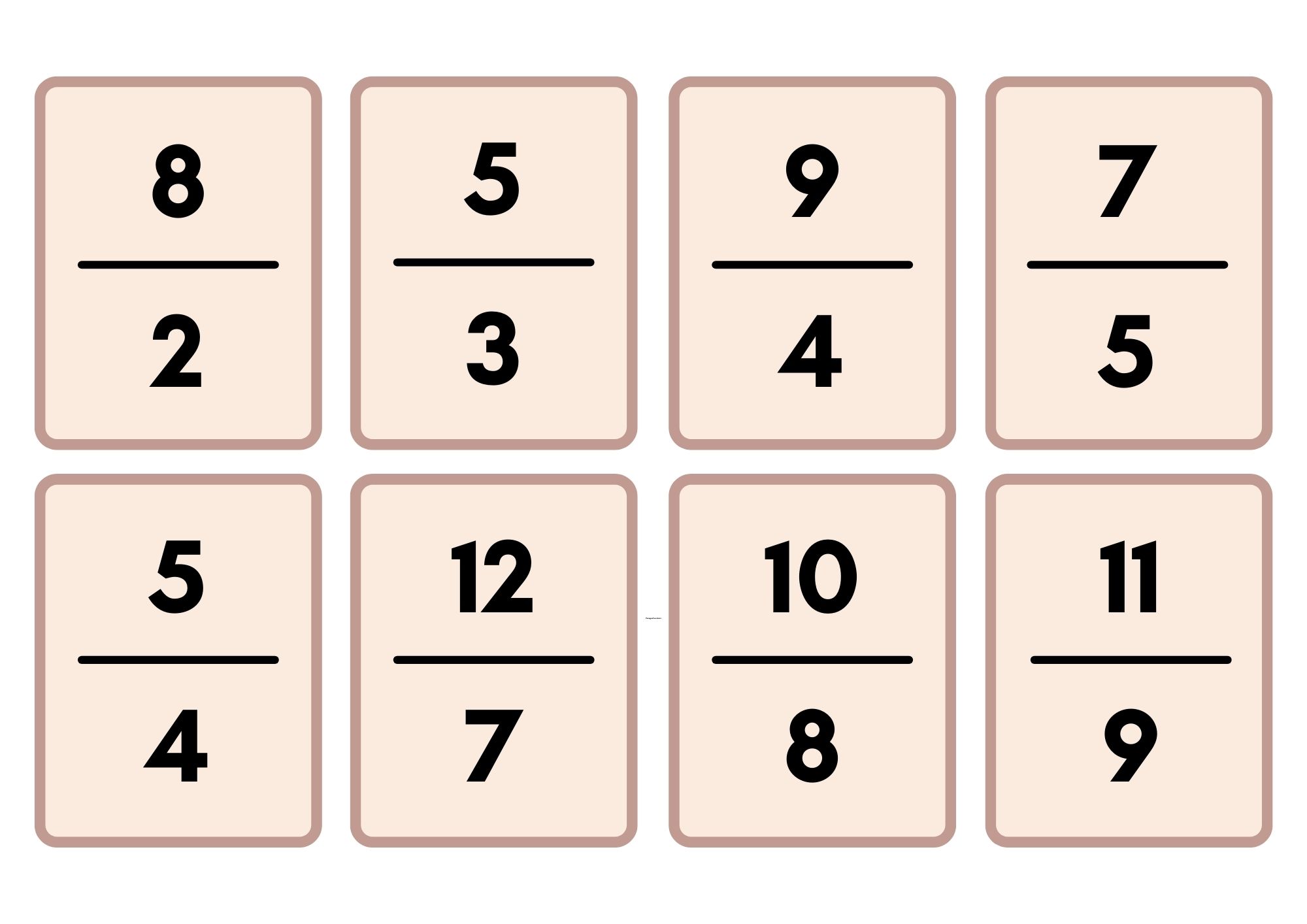
Tam Sayılı Kesirlere Örnekler:
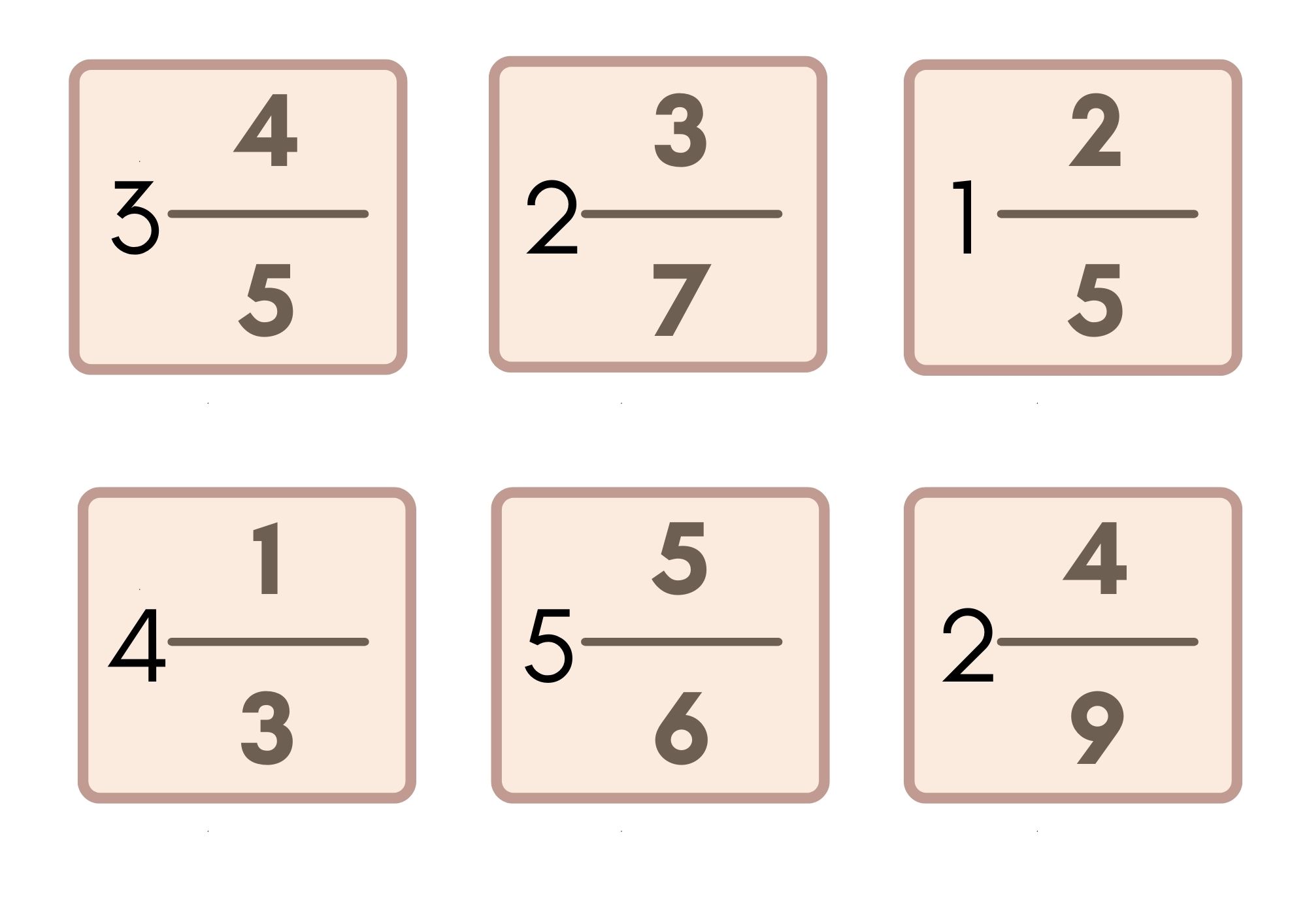
Bileşik Kesri Tam Sayılı Kesre Çevirme
Bilgi: Bileşik kesri tam kısımlı kesre çevirirken bileşik kesrin payını paydasına böleriz. Bölme işleminin sonucunda;
- Bölüm tam kısımlı kesrin tam kısmına
- Kalan tam kısımlı kesrin payına
- Bölen ise tam kısımlı kesrin paydasına yazılır.
Örneğin; \dfrac{13}{5} bileşik kesrini tam kısımlı kesre çevirelim.
✅ Payı paydaya böleriz.
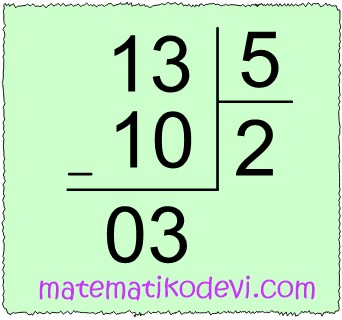
✅ Bölüm tam kısımlı kesrin tam kısmına, Kalan tam kısımlı kesrin payına, Bölen ise tam kısımlı kesrin paydasına yazılır.
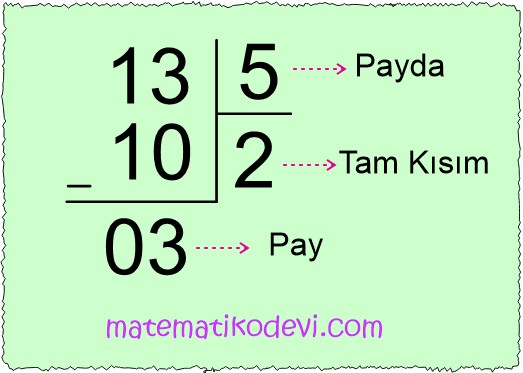
✅ \dfrac{13}{5} bileşik kesrinin tam sayılı kesre çevrilmiş hali 2 \dfrac{3}{5}
Tam Sayılı Kesri Bileşik Kesre Çevirme
Bilgi: Tam sayılı kesri bileşik kesre çevirirken;
- Tam sayılı kesrin paydası ile tam kısmı çarpılır.
- Çarpıma tam kısımlı kesrin payını ekleriz.
- Bulduğumuz sonucu paya yazarız.
- Paydayı ise aynen yazarız.
Örneğin; 4 \dfrac{3}{5} tam sayılı kesri bileşik kesre çevirelim.
✅ Tam sayılı kesrin paydası ile tam kısmı çarpılır.
5×4=20
✅ Çarpıma tam kısımlı kesrin payını ekleriz.,
20+3=23
✅ Bulduğumuz sonucu paya yazarız, Paydayı ise aynen yazarız.
\dfrac{23}{5}✅ 4 \dfrac{3}{5} tam sayılı kesrin bileşik kesre çevrilmiş hali \dfrac{23}{5} olur.

Cevaplar: \dfrac{3}{2} , \dfrac{19}{4} , \dfrac{17}{3} , \dfrac{49}{5} , \dfrac{22}{3} , \dfrac{30}{7}
Bileşik Kesirleri Sayı Doğrusunda Gösterme
Bilgi: Bileşik kesirleri sayı doğrusunda gösterirken;
- Bileşik kesrin kaç tane birim kesirden oluştuğuna bakarız.
- Sonra sayı doğrusunda sıfırdan başlayıp kaç tane birim kesirden oluştuysa (pay), o kadar birim kesir ilerleriz.
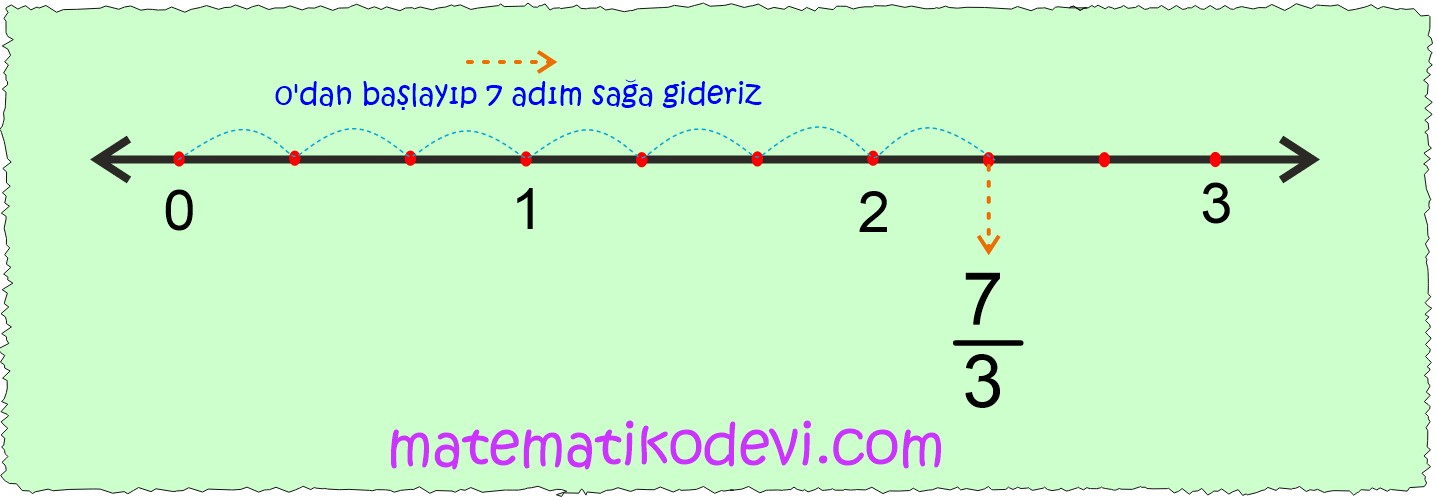
Örneğin; \dfrac{7}{3} bileşik kesrini sayı doğrusunda gösterelim.
✅ Bileşik kesrin kaç tane birim kesirden oluştuğuna bakarız.
\dfrac{7}{3} bileşik kesri 7 tane \dfrac{1}{3} birim kesrinden oluşmaktadır.
✅ Sonra sayı doğrusunda sıfırdan başlayıp kaç tane birim kesirden oluştuysa (pay), o kadar birim kesir ilerleriz.
0’dan başlayıp 7 tane \dfrac{1}{3} ilerleriz.
Tam Sayılı Kesirlerin Sayı Doğrusunda Gösterilmesi
Bilgi: Tam sayılı kesirleri sayı doğrusunda gösterirken;
- 0’dan başlayıp tam kısım kadar ilerleriz. ( ardışık sayıların arasını parçalara ayırmayız)
- Sonra geldiğimiz bütünü payda kadar eşit parçaya ayırıp, pay kadar ilerleriz.
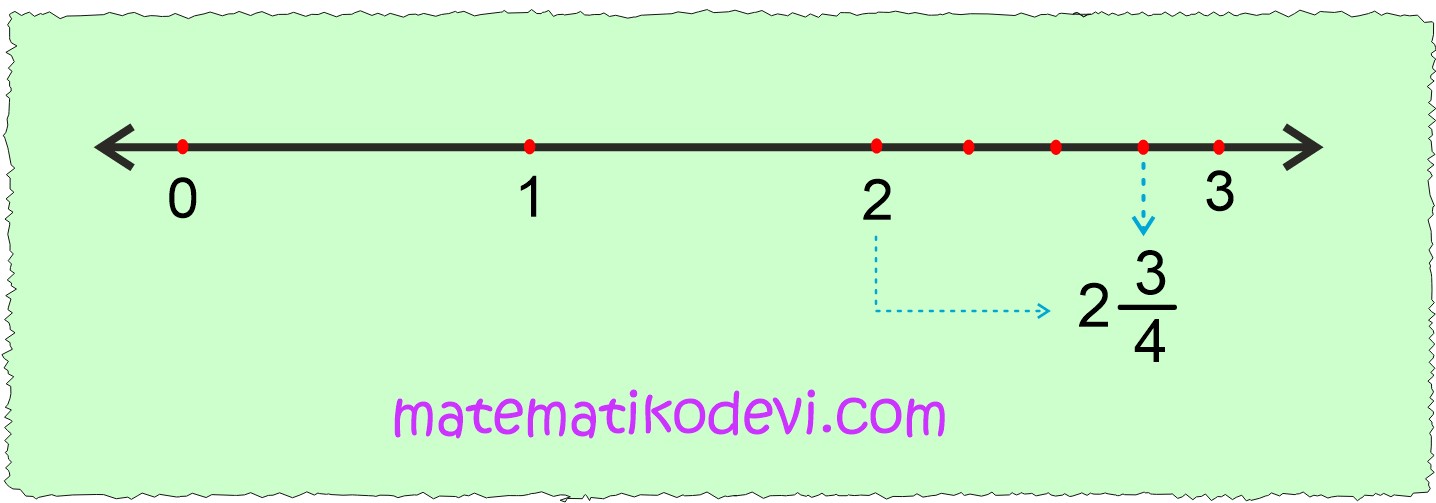
Örneğin; 2 \dfrac{3}{4} tam sayılı kesrini sayı doğrusunda gösterelim.
✅ 0’dan başlayıp tam kısım kadar ilerleriz. ( ardışık sayıların arasını parçalara ayırmayız)
2 \dfrac{3}{4} tam sayılı kesrin tam kısmı 2 olduğu için sıfırdan başlayıp 2 adım ilerleriz.

✅ Sonra geldiğimiz bütünü payda kadar eşit parçaya ayırıp, pay kadar ilerleriz.
2 ile 3 arasını 4 parçaya ayırıp 3 adım ilerleriz.
🔻 Diğer konulara hızlı geçiş 🚀
| ⏪ Önceki Konu | Sonraki Konu ⏩ |
| BİRİM KESİRLERİ SAYI DOĞRUSUNDA GÖSTERME VE SIRALAMA | Bir Doğal Sayı ile Bir Bileşik Kesrin Karşılaştırılması |

