Ondalık Gösterimleri Rasyonel Sayıya Çevirme
Kazanım: Devirli olan ve olmayan ondalık gösterimleri rasyonel sayı olarak ifade eder.
Ondalık Gösterimleri Rasyonel Sayıya Çevirme işlemlerini yapabilmek için aşağıda ki başlıkları kontrol edebilirsiniz.
Bu konuda neler öğreneceğiz :
Ondalık Gösterimleri Rasyonel Sayıya Çevirme
Ondalık gösterimler devirli olmayan ondalık gösterim ve devirli olan ondalık gösterim olmak üzere ikiye ayrıldığını öğrenmiştik. Ondalık gösterimleri rasyonel yani kesir çizgisi kullanarak ifade etmeyi devirli olmayan ondalık gösterimleri rasyonel olarak ifade etme ve devirli olan ondalık gösterimleri rasyonel olarak ifade etme olmak üzere iki başlıkta inceleyeceğiz.
Devirli Olmayan Ondalık Sayıların Rasyonel Sayı Olarak Gösterimi
Devirli olmayan ondalık sayıyı rasyonel sayıya çevirirken aşağıdaki adımları izleriz.
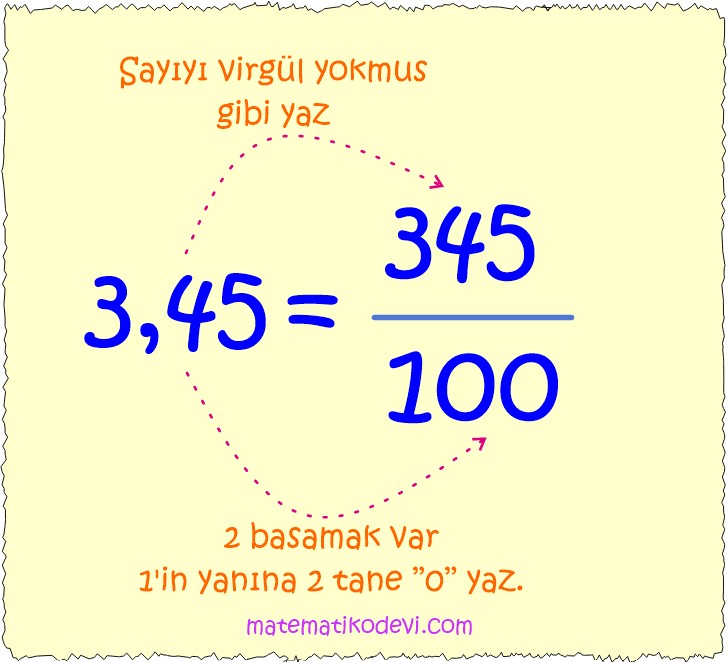
✅ Ondalık sayıyı virgül yokmuş gibi yaz.
✅ Virgülden sonraki basamak sayısı kadar 1’in yanına 0 yaz.
Örnek: Aşağıda verilen ondalık gösterimleri rasyonel olarak yazılışlarını inceleyelim.
➡️ 0,9 sayısının rasyonel olarak gösterimi 👉 \dfrac{9}{10}
➡️ 1,5 sayısının rasyonel olarak gösterimi 👉 \dfrac{15}{10}
➡️ 2,567 sayısının rasyonel olarak gösterimi 👉 \dfrac{2567}{1000}
➡️ 0,14 sayısının rasyonel olarak gösterimi 👉 \dfrac{14}{100}
Ondalık gösterimleri rasyonel sayıya çevirme yaparken ikinci bir yöntem olarak aşağıda görselde verilen yöntemi de kullanabiliriz.

Devirli Ondalık Sayıların Rasyonel Sayı Olarak Gösterimi
Devirli ondalık gösterimleri rasyonel sayıya çevirmek için devirli ondalık sayıda devreden kısım ve devretmeyen kısım neresi olduğunu bilmemiz gerekir.
Devreden kısım: Devirli ondalık sayıda üzerinde çizgi olan kısma devreden kısım denir.
Örneğin; 2,5 \overline{17} devirli ondalık sayısında 17 dereden kısımdır.
Devretmeyen kısım: Devirli ondalık sayıyı virgül yokmuş gibi düşünüp üzerinde çizgi olmayan kısma devretmeyen kısım denir.
Örneğin; 2,5 \overline{17} devirli ondalık sayısında 25 devretmeyen kısımdır.
Sayının Tamamı: Sayının tamamı denildiği zaman sayıyı virgül yokmuş gibi düşünürüz.
Örneğin; 2,5 \overline{17} devirli ondalık sayısında sayının tamamı denildiğinde 2517 yazarız.
📌 Devirli ondalık sayıyı rasyonel sayı olarak göstermek için aşağıdaki adımları takip ederiz.
- Sayının tamamından devretmeyen kısmı çıkarırız. Bulduğumuz sonucu pay olarak yazarız.
- Virgülden sonra devreden rakam kadar 9 , devretmeyen rakam kadar 0 atarız. Bulduğumuz sayıyı paydaya yazarız.
Örneğin; 1,4 \overline{5} devirli ondalık sayısını rasyonel sayı olarak yazalım.
➡️ Sayının tamamından devretmeyen kısmı çıkarırız
145-14=131 (bulduğumuz sonuç paya yazılır.)
➡️ Virgülden sonra devreden rakam kadar 9 , devretmeyen rakam kadar 0 atarız.
Virgülden sonra 1 tane devreden 1 tanede devretmeyen rakam var. Bu yüzden 1 tane 9 1 tane 0 atarız.
Yani paydaya 90 yazarız.
1,4 \overline{5} devirli ondalık sayısının rasyonel sayı olarak gösterimi \dfrac{131}{90} olur.

Örnek: Aşağıda verilen devirli ondalık sayıları rasyonel sayı olarak yazalım.
✅ 32, \overline{7} = ❓
➡️ Sayının tamamından devretmeyen kısmı çıkarırız
327-32=295 (bulduğumuz sonuç paya yazılır.)
➡️ Virgülden sonra devreden rakam kadar 9 , devretmeyen rakam kadar 0 atarız
Virgülden sonra 1 tane devreden var ve devretmeyen kısım yok. Bu yüzden 1 tane 9 yazarız.
Yani paydaya 9 yazarız.
32, \overline{7} devirli ondalık sayısının rasyonel sayı olarak gösterimi \dfrac{295}{9} olur.
✅ 0,13 \overline{2} = ❓
➡️ Sayının tamamından devretmeyen kısmı çıkarırız
132-13=119 (bulduğumuz sonuç paya yazılır.)
➡️ Virgülden sonra devreden rakam kadar 9 , devretmeyen rakam kadar 0 atarız
Virgülden sonra 1 tane devreden 2 tanede devretmeyen rakam var. Bu yüzden 1 tane 9 ,2 tane 0 atarız.
Yani paydaya 900 yazarız.
0,13 \overline{2} devirli ondalık sayısının rasyonel sayı olarak gösterimi \dfrac{119}{900} olur.
✅ 2,1 \overline{43} = ❓
➡️ Sayının tamamından devretmeyen kısmı çıkarırız
2143-21=2122 (bulduğumuz sonuç paya yazılır.)
➡️ Virgülden sonra devreden rakam kadar 9 , devretmeyen rakam kadar 0 atarız
Virgülden sonra 2 tane devreden 1 tanede devretmeyen rakam var. Bu yüzden 2 tane 9 ,1 tane 0 atarız.
Yani paydaya 990 yazarız.
2,1 \overline{43} devirli ondalık sayısının rasyonel sayı olarak gösterimi \dfrac{2122}{990} olur.
Ondalık Gösterimleri Rasyonel Sayıya Çevirme
Ondalık Gösterimleri Rasyonel Sayıya Çevirme konusu ile aşağıdaki test ve etkinlikleri çözerek konuyu pekiştirebilirsiniz.
İnternet hızından kaynaklı test ve etkinlikler açılmamış olursa sayfayı yenileyiniz.
Ondalık Gösterimleri Rasyonel Sayıya Çevirme konusu burada bitmiştir. Konuyu pekiştirmek için online etkinliklerimizi kullanabilirsiniz.
🔻 Diğer konulara hızlı geçiş 🚀
| ⏪ Önceki Konu | Sonraki Konu ⏩ |
| Rasyonel Sayıların Ondalık Gösterimi Ve Devirli Ondalık Sayılar | Rasyonel Sayıları Karşılaştırma ve Sıralama |

