Birinci Dereceden Bir Bilinmeyenli Denklemler 7.Sınıf
Kazanım : Birinci dereceden bir bilinmeyenli denklemi tanır ve verilen gerçek hayat durumlarına uygun birinci dereceden bir bilinmeyenli denklem kurar.
Bu konuda neler öğreneceğiz :
Birinci Dereceden Bir Bilinmeyenli Denklemler
İçinde bilinmeyen bulunan eşitliklere denklem denir. Burada bilinmeyenin kuvveti (derecesi) bir ise ve sadece bir bilinmeyen varsa bu denklemler birinci dereceden bir bilinmeyenli denklemler olarak adlandırılır.
3x+5 ➡️ Denklem değil cebirsel ifadedir. Denklem olması için eşittir ifadesi ve eşittir ifadesinin karşısında eşitlik olmalıdır.
5x2 + 3 = 20 ➡️ İkinci dereceden bir bilinmeyenli denklemdir.
2x + 5y =10 ➡️ Birinci dereceden iki bilinmeyenli denklemdir.
4x+3=19 ➡️ Denklem
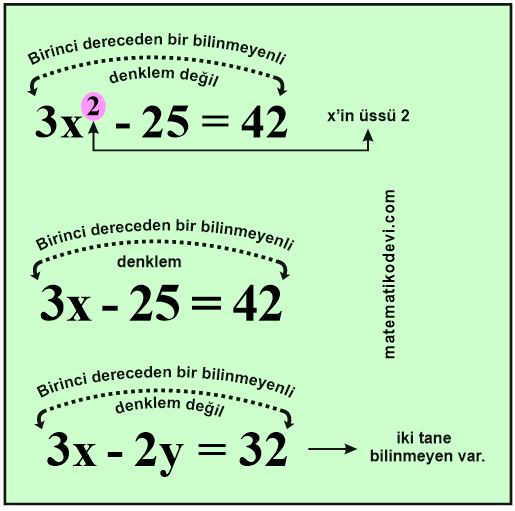
Bir ifadenin birinci dereceden bir bilinmeyenli denklem olabilmesi için;
- 1 tane bilinmeyenden (harften) oluşmalı
- Eşitlik olmalı
- Bilinmeyenin (harfin) üssü 1 olmalı
Verilen Sözel İfadeyi Denkleme Çevirme
Sözel durumlara uygun denklemleri kurarken, bilinmeyenlere harfler ya da semboller verilerek matematik diline çevrilir.
Örneğin; ‘’Bir sayının 4 katının 5 eksiği 15’tir.’’ Sözel ifadesine ait denklemi kuralım.
Sayı: x olsun
4 katı : 4x
4 katının 5 eksiği: 4x – 5
Denklem: 4x – 5 = 15
Örneğin; ‘’Bir sayının 8 fazlasının yarısı 18’dir.’’ Sözel ifadesine ait denklemi kuralım.
Sayı: x olsun
Sayının 8 fazlası: x+8
Sayının 8 fazlasının yarısı: \dfrac{x+8}{2}
Denklem: \dfrac{x+8}{2} = 18
Birinci Dereceden Bir Bilinmeyenli Denklemler Test
Birinci dereceden bir bilinmeyenli denklemler testini çözmek için aşağıya tıklayın. Test internet hızınızdan kaynaklı açılmamış olursa sayfayı yenileyiniz.
🔻 Diğer konulara hızlı geçiş 🚀
| ⏪ Önceki Konu | Sonraki Konu ⏩ |
| Eşitliğin Korunumu İlkesi | Denklem Çözme |

