Denklem Çözme Konu Anlatımı 7.Sınıf
Kazanım: Birinci dereceden bir bilinmeyenli denklemleri çözer.
Bu konuda neler öğreneceğiz :
Denklem Çözme Konu Anlatımı
Bir eşitlikte eşitliğin her iki tarafına aynı işlem uygulandığımızda eşitlik bozulmaz. O zaman denklemde eşitliğin her iki tarafına aynı sayı eklenir, her iki tarafından aynı sayı çıkarılır, her iki tarafı aynı sayıyla çarpılır veya bölünürse eşitlik bozulmaz.
Denklemi çözerken aşağıdaki adımları kullanırız.
➡️ Denklemde toplama işlemi varsa bilinmeyenle toplam durumundaki sayı eşitliğin her iki tarafından çıkarılır. Bu şekilde denklem sadeleştirilmiş olur.

➡️ Denklemde çıkarma işlemi varsa bilinmeyenden çıkarılan sayı eşitliğin her iki tarafına eklenir. Bu şekilde denklem sadeleştirilmiş olur.
➡️ Denklem sadeleştirildiğinde denklemde çarpma işlemi varsa denklemin her iki tarafı bilinmeyenin kat sayısına bölünür. ve bilinmeyenin değeri bulunmuş olur.

➡️ Denklem sadeleştirildiğinde denklemde bölme işlemi varsa denklemin her iki tarafı da bilinmeyenin bölündüğü sayı ile çarpılır ve bilinmeyenin değeri bulunmuş olur.
ÖRNEK: 4x + 5 = 29 işlemini yapalım.
➡️ Denklemde çıkarma işlemi varsa bilinmeyenden çıkarılan sayı eşitliğin her iki tarafına eklenir. Bu şekilde denklem sadeleştirilmiş olur.
4x + 5 = 29
4x + 5-5 = 29-5
4x = 24
➡️ Denklem sadeleştirildiğinde denklemde çarpma işlemi varsa denklemin her iki tarafı bilinmeyenin kat sayısına bölünür. ve bilinmeyenin değeri bulunmuş olur.
4x = 24
x = 24/4
x = 6
Denklemin kökü 6 bulunur. Çözüm kümesi Ç = {6}
ÖRNEK:

➡️ Denklemde çıkarma işlemi varsa bilinmeyenden çıkarılan sayı eşitliğin her iki tarafına eklenir. Bu şekilde denklem sadeleştirilmiş olur.
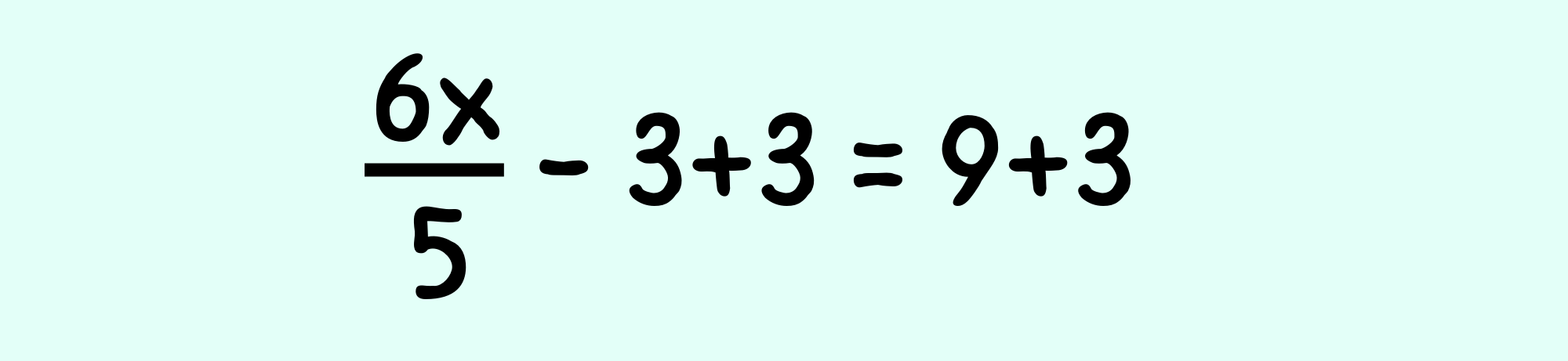

➡️ Denklem sadeleştirildiğinde denklemde bölme işlemi varsa denklemin her iki tarafı da bilinmeyenin bölündüğü sayı ile çarpılır.

➡️ Denklem sadeleştirildiğinde denklemde çarpma işlemi varsa denklemin her iki tarafı bilinmeyenin kat sayısına bölünür. ve bilinmeyenin değeri bulunmuş olur.
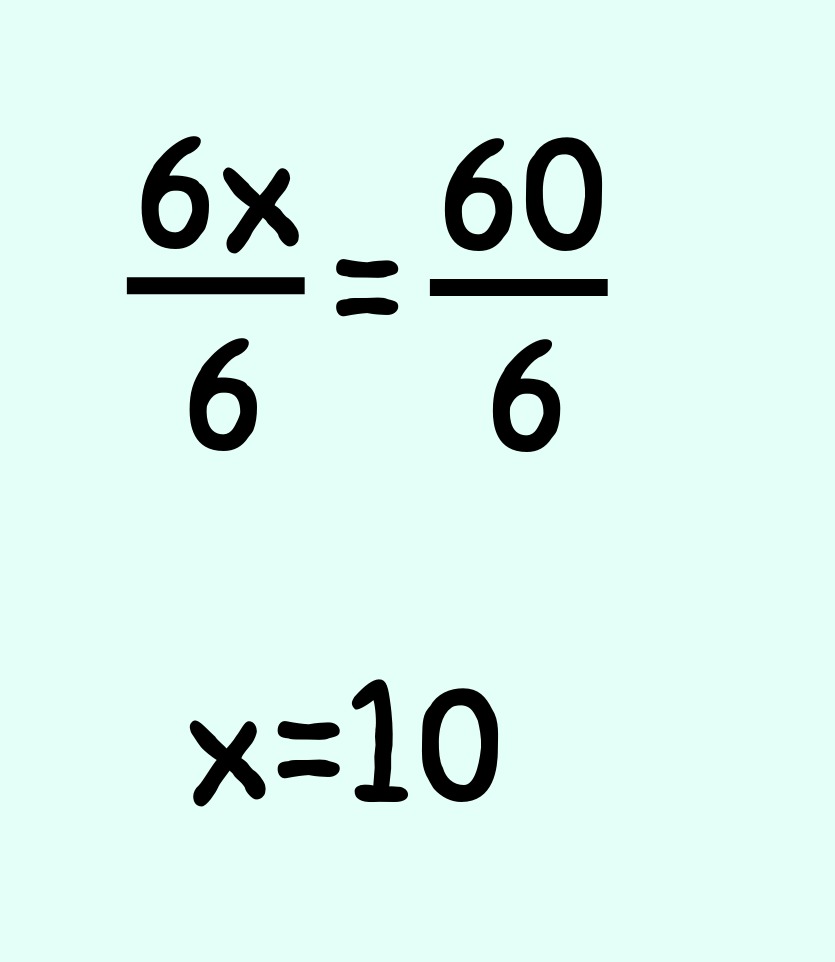
ÖRNEK: 3.(x-1) = 12 ise x değerini bulalım.
➡️ Her iki tarafı x’in katsayısına bölelim.
\dfrac{3.(x-1)}{3} = \dfrac{12}{3}
➡️ Her iki tarafa 1 ekleyelim ve x’in değerini bulalım.
x-1 = 4
x-1+1 =4+1
x=5
Denklem Çözme Test
Denklem çözme testini çözmek için aşağıya tıklayın.
Test internet hızınızdan kaynaklı açılmamış olursa sayfayı yenileyiniz.
🔻 Diğer konulara hızlı geçiş 🚀
| ⏪ Önceki Konu | Sonraki Konu ⏩ |
| Birinci Dereceden Bir Bilinmeyenli Denklemler |

