Kesirlerde Sıralama Konu Anlatımı
Kazanım: Payları veya paydaları eşit kesirleri sıralar.
Bu konuda neler öğreneceğiz :
Paydaları Eşit Kesirleri Sıralama
Bilgi: Paydaları eşit olan kesirlerde payı büyük olan kesir daha büyük, payı küçük olan kesir daha küçüktür.
Örneğin;
\dfrac{8}{9} , \dfrac{10}{9} , \dfrac{7}{9} kesirlerini küçükten büyüğe doğru sıralayalım.
Kesirlerin paydası eşit olduğu için en küçük kesir payı küçük olan kesirdir.
\dfrac{7}{9} < \dfrac{8}{9} < \dfrac{10}{9}
Kesirleri kaç adet birim kesirden oluştuğunu hesaplayarak da sıralama yapabiliriz.
➡️ \dfrac{7}{9} kesri 7 tane birim kesirden oluşur. (7 tane \dfrac{1}{9} )
➡️ \dfrac{8}{9} kesri 8 tane birim kesirden oluşur. (8 tane \dfrac{1}{9} )
➡️ \dfrac{10}{9} kesri 10 tane birim kesirden oluşur. (10 tane \dfrac{1}{9} )
Kesirlerde sıralamayı daha iyi anlamak için aşağıdaki pasta örneği gibi yorumlayabiliriz.
Örneğin bir pastayı 8 eşit dilime ayıralım.
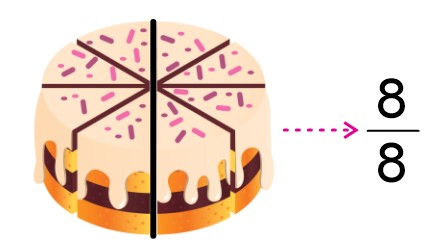
İki arkadaşın bu pastalardan bazı dilimlerini yemiş ve geriye kalan dilimleri aşağıdaki gibidir. geriye kalan dilimlerden hangisinin daha büyük olduğunu bulalım.
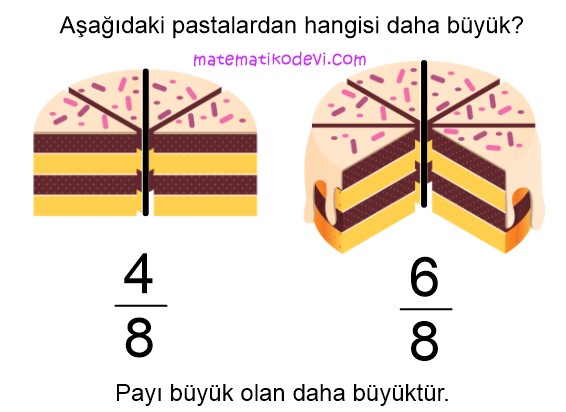
Yukarıdaki karşılaştırmada \dfrac{6}{8} > \dfrac{4}{8} olduğunu görürüz.
Pasta örneğinden de görüldüğü gibi paydaları eşit olan kesirlerde payı büyük olan daha büyüktür.
Payları Eşit Olan Kesirleri Sıralama
Bilgi: Payları eşit olan kesirlerde payı büyük olan kesir daha küçük, payı küçük olan kesir daha büyüktür.
Örneğin;
\dfrac{7}{6} , \dfrac{7}{5} , \dfrac{7}{9} kesirlerini küçükten büyüğe doğru sıralayalım.
Kesirlerin payları eşit olduğu için en küçük kesir paydası büyük olan kesirdir.
\dfrac{7}{9} < \dfrac{7}{6} < \dfrac{7}{5}
Kesirleri kaç adet birim kesirden oluştuğunu hesaplayarak da sıralama yapabiliriz.
➡️ \dfrac{7}{9} kesri 7 tane \dfrac{1}{9} oluşur.
➡️ \dfrac{7}{6} kesri 7 tane \dfrac{1}{6} oluşur.
➡️ \dfrac{7}{5} kesri 7 tane \dfrac{1}{5} oluşur.
Birim kesirleri sıralarsak \dfrac{1}{9} < \dfrac{1}{6} < \dfrac{1}{5}
Birim kesirlerden yararlanıp \dfrac{7}{9} < \dfrac{7}{6} < \dfrac{7}{5} sırlamasını elde ederiz.
Bilgi: Tam sayılı kesirlerde tam kısmı büyük olan kesir daha büyüktür.
Örneğin; 3 \dfrac{4}{5} kesri ile 4 \dfrac{1}{5} kesrini karşılaştırırken tam kısımlarına bakarız.
3<4 olduğu için 3 \dfrac{4}{5} < 4 \dfrac{1}{5} olur.
Bilgi: Tam sayılı kesirlerde tam kısmı eşit ise kesir kısmını karşılaştırırız.
Örneğin; 5 \dfrac{3}{5} kesri ile 5 \dfrac{1}{5} kesrini karşılaştırırken tam kısımlarına bakarız.
Tam kısımları eşit (5=5 ) olduğu için kesirlere bakarız.
Kesirleri karşılaştırırsak \dfrac{1}{5} < \dfrac{4}{5}
O zaman sıralama 5 \dfrac{1}{5} < 5 \dfrac{4}{5} şeklinde olur.
Paydası Diğerinin Katı Olan Kesirleri Sıralama
Bilgi: Birinin paydası diğerinin paydasının katı olan kesirleri karşılaştırmak için önce, sadeleştirme veya genişletme yapılarak kesirlerin paydaları eşitlenir. Sonra paydaları eşitlenen kesirlerden payı büyük olan kesir daha büyük, payı küçük olan kesir daha küçük olur.
Örneğin;
\dfrac{5}{4} , \dfrac{9}{8} kesirlerini küçükten büyüğe doğru sıralayalım.
➡️ Kesirlerin paydalarını sadeleştirme veya genişletme yaparak eşitleriz.
\dfrac{5}{4} 👉kesrini 2 ile genişletelim.
\dfrac{5×2}{4×2} = \dfrac{10}{8}
\dfrac{9}{8} < \dfrac{10}{8}
\dfrac{10}{8} kesri \dfrac{5}{4} kesrine denktir.
O zaman \dfrac{9}{8} < \dfrac{5}{4} şeklinde sıralama yaparız.
Kesirlerde Karşılaştırma Etkinlik:

Kesirlerde Karşılaştırma Etkinlik Cevap Anahtarı:
Aşağıdaki yöntemde matematik ödevi sitesine özel farklı bir yöntem anlatılmıştır. İzlemenizi tavsiye ederim.
Kesirlerde Sıralama Konu Anlatımı burada bitmiştir. Kendinizi değerlendirmek için aşağıdaki etkinlikleri çözebilirsiniz. Etkinlikler yüklenmemiş ise sayfayı yenileyiniz.
Kesirlerde Sıralama 5.sınıf Test
🔻 Diğer konulara hızlı geçiş 🚀
| ⏪ Önceki Konu | Sonraki Konu ⏩ |
| DENK KESİRLER | Bir Çokluğun İstenen Kesir Kadarını Bulma |

