En Çok Üç Basamaklı İki Doğal Sayının Çarpma İşlemi Yapma
Kazanım: En çok üç basamaklı iki doğal sayının çarpma işlemini yapar.
Bu konuda neler öğreneceğiz :
En Çok Üç Basamaklı İki Doğal Sayının Çarpma İşlemi
Çarpma İşlemi
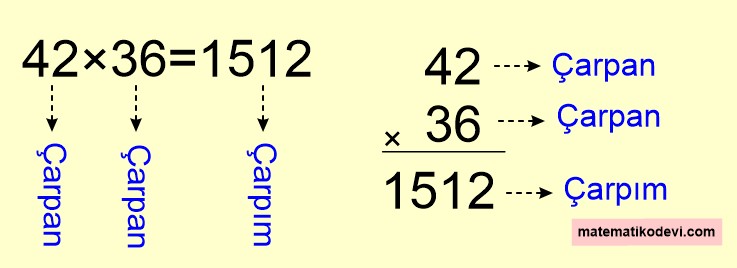
Bilgi: Çarpma işleminde çarpılan sayılara çarpan, sonuca ise çarpım denir. Çarpma işlemi × veya · işaretiyle gösterilir.
Çarpma işlemi bir sayının tekrarlı toplamı demektir. Örneğin 4 ile 20 sayısını çarpmak (4×20) demek 4 tane 20’yi toplamak (20+20+20+20) demektir. Aslında çarpma işlemi toplama işleminin özel bir hali olmuş oluyor.
En çok üç basamaklı iki doğal sayının çarpımını hesaplarken aşağıdaki adımları takip ederiz.👇
- Çarpma işlemine ikinci çarpanın birler basamağı ile başlanır.
- Birler basamağındaki rakam birinci çarpan ile çarpılır. Elde edilen sayı sayıların altında çarpım kısmına yazılır.
- Sonra ikinci çarpanın onlar basamağı ile devam edilir. İkinci çarpanın onlar basamağı ile birinci çarpan çarpılır. Elde edilen sayı önceki bulduğumuz sonucun altına bir basamak sola kaydırılarak yazılır.
- İkinci çarpanda yüzler basamağı varsa aynı işlem uygulanır.
- Bulunan sayılar toplanarak çarpım elde edilir.
Örneğin 358×24 çarpma işlemini yukarıdaki adımlara göre çarpalım.
➡️ Çarpma işlemine ikinci çarpanın birler basamağı ile başlanır.
Bu adımda ikinci çarpanın birler basamağı olan 4 ile birinci çarpan olan 358 sayısını çarparız. Elde edilen 1432 sayısı sayıların altında çarpım kısmına yazılır.

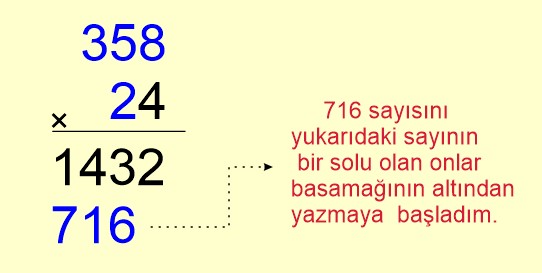
➡️ Sonra ikinci çarpanın onlar basamağı ile devam edilir. İkinci çarpanın onlar basamağı ile birinci çarpan çarpılır. Elde edilen sayı önceki bulduğumuz sonucun altına bir basamak sola kaydırılarak yazılır.
Bu adımda ikinci çarpanın onlar basamağı olan 2 ile birinci çarpan olan 358 sayısını çarparız. Elde ettiğimiz 716 sayısının önceki bulduğumuz sonucun (1432) altına bir basamak sola kaydırılarak yazarız.
➡️ İkinci çarpanda yüzler basamağı varsa aynı işlem uygulanır.
İkinci çarpanda yüzler basamağı olmadığı için diğer adıma geçilir.
➡️ Bulunan sayılar toplanarak çarpım elde edilir.
Bu adımda alt alta yazdığımız sayıları toplayıp çarpımı (sonucu) elde ederiz.
Toplama yaparken sayıyı sola kaydırdığımız için basamağın altında boşluk oluştu. Oluşan bu boşluğu sıfır gibi düşünüp toplama yaparız. Yani toplama yaparken 2’nin altında bir rakam olmadığı için 2’nin altında sıfır varmış gibi düşünüp 2 ile sıfırı (2+0) toplarız.

🤔 2.satırda bir basamak sola kaydırmamızın sebebi nedir?
🤓 Yukarıdaki işlemde 2.satırda 2 ile 358 sayısını çarptık. Normalde bu işlemi 20 ile 358 çarparak yapmamız gerekecekti. Bunun yerine 2. satırda basamağı bir sola kaydırıp 2 ile 358 ‘i çarptık.
Örnek: 685×42 işleminin sonucunu bulalım.
➡️ 685’i üste , 42’yi alta yazalım.
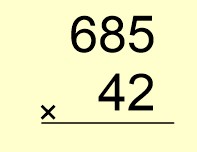
➡️ 685’i 42’nin birler basamağındaki rakam ile çarpalım.
685×2=1370
Bulduğumuz sayıyı alta yazalım.
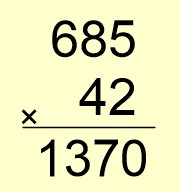
➡️ 685’i 42’nin onlar basamağındaki rakam ile çarpalım.
685×4=2740
Bulduğumuz sayıyı bir basamak sola kaydırarak yazalım.

➡️ Elde ettiğimiz sonuçları toplayalım.
Toplarken 1370 sayısının birler basamağının altında 0 (sıfır) olduğunu varsayalım.

🎭 Biraz Eğlenelim 🎭 – Japon Çarpma Tekniği
42×35 işlemini Japon çarpma tekniğine göre yapalım.
➡️ 42 sayısını 4 tene ve 2 tane karşılıklı çizgi çizerek gösterelim.
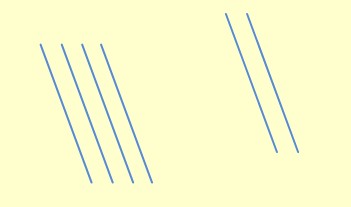
➡️ 35 sayısını göstermek için 3 ve 5 tane çizgi çizelim. önceki çizdiğimiz çizgileri kesecek şekilde.
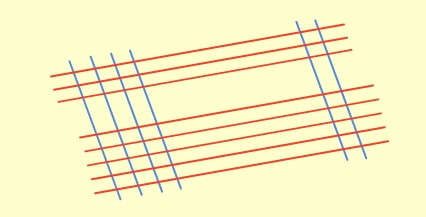
➡️ Çizgilerin kesim yerlerini işaretleyelim.
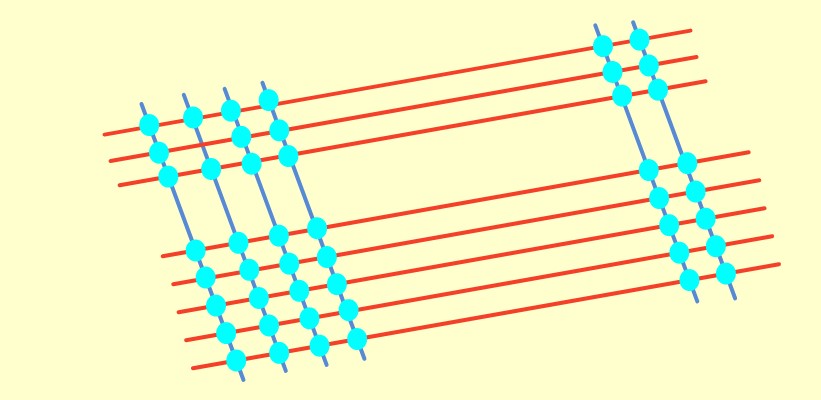
➡️ Aynı hizadakileri basamak olacak şekilde noktaları sayalım.
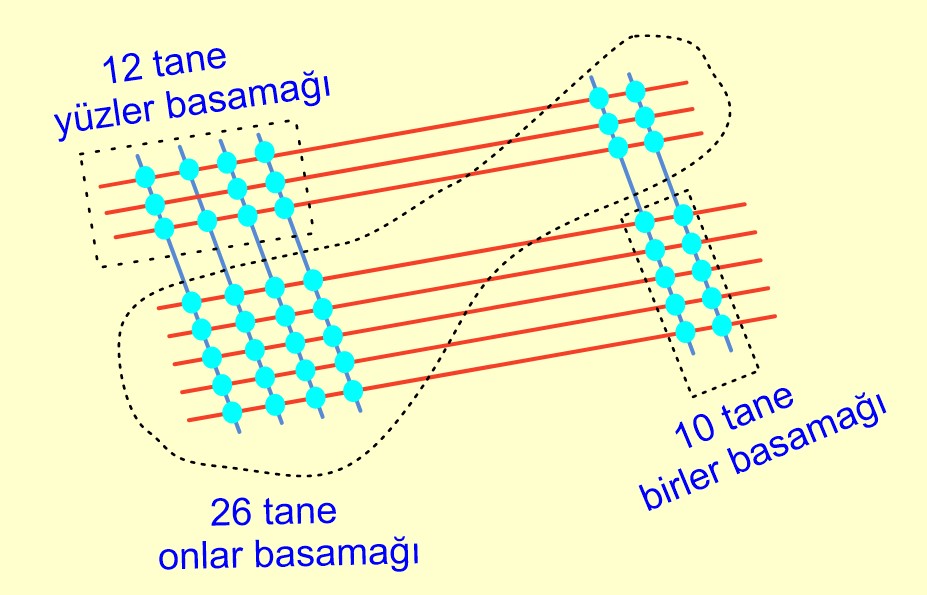
➡️ Sağdan başlayıp eldeyi bir sonraki basamağa ekleyelim ve sonucu yazalım.
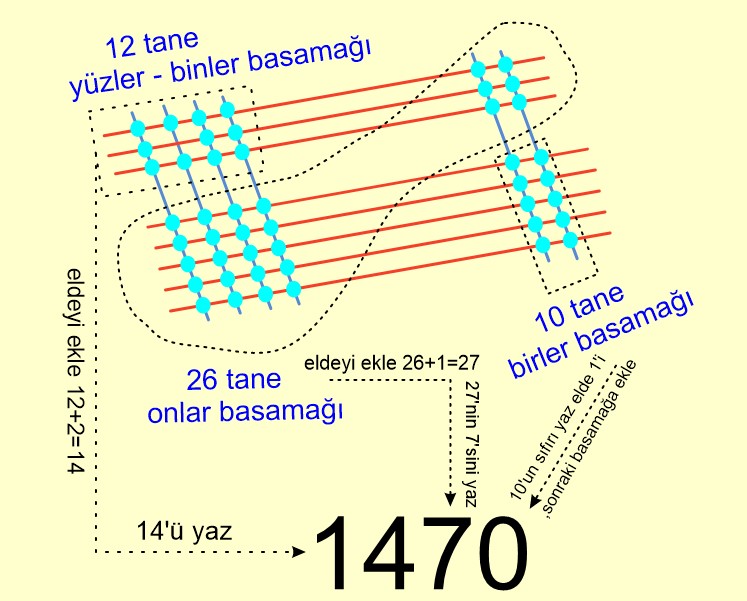
🤓 42×35 işleminin sonucu 1470’dir.
En Çok Üç Basamaklı İki Doğal Sayının Çarpma İşlemi Test
Aşağıdaki En Çok Üç Basamaklı İki Doğal Sayının Çarpma İşlemi konusu ile ilgili testi çözerek konuyu pekiştirebilirsiniz. İnternet hızınızdan kaynaklı test yüklenmemiş olursa sayfayı yenileyiniz.
En Çok Üç Basamaklı İki Doğal Sayının Çarpma İşlemi konusu burada bitmiştir. Konu test ve etkinliklerine göz atabilirsiniz.
🔻 Diğer konulara hızlı geçiş 🚀
| ⏪ Önceki Konu | Sonraki Konu ⏩ |
| Toplama Ve Çıkarma İşlemlerinin Sonucunu Tahmin Etme | Doğal Sayılarda Bölme İşlemi |

