Orantı Nedir ?
Bu konuda neler öğreneceğiz :
Orantı Nedir ?
Bu yazı içerisinde Oran-Orantı konu anlatımının 2.bölümü olan orantı hakkında bilgi sahibi olacaksınız.
Kazanım: Gerçek hayat durumlarını inceleyerek iki çokluğun orantılı olup olmadığına karar verir.
Orantı Nedir ?
Bilgi: İki veya daha fazla oranın eşitliğine orantı denir.
Orantıyı ;
✅ \dfrac{a}{b} = \dfrac{c}{d}
✅ a÷b = c÷d
✅ a/b = c/d
şeklinde gösterebiliriz.
Örneğin;
\dfrac{2}{5} = \dfrac{8}{20} eşitliği orantıdır.
✅ \dfrac{2}{5} oranının 4 ile genişlettiğimizde
✅ \dfrac{8}{20} olduğuna dikkat ettiniz mi?
Bilgi: Orantıda içlerde bulunan sayıların çarpımı dışlarda bulunan sayıların çarpımına eşittir.
✅ \dfrac{a}{b} = \dfrac{c}{d} orantısında b ile c içler, a ile d dışlardır.
Orantıda içte bulunan sayılar içler, dışta bulunan sayılara dışlar denir.
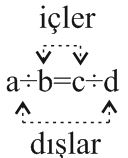
Örnek: \dfrac{x}{12} = \dfrac{10}{3} orantısında x’in değerini bulalım.
✅ \dfrac{x}{12} = \dfrac{10}{3} orantısında içler dışlar çarpımı yapalım.
x.3=12.10
3x=120
x=40
Örnek: \dfrac{6}{2x-3} = \dfrac{2}{5} orantısında x’in değerini bulalım.
✅ \dfrac{6}{2x-3} = \dfrac{2}{5} orantısında içer dışlar çarpımı yapalım.
2.(2x-3)=6.5
4x-6=30
4x=36
x=9
Örnek: \dfrac{12}{10} oranı ile \dfrac{20}{15} oranı bir orantı oluşturur mu?
✅ \dfrac{12}{10} = \dfrac{20}{15} orantı oluşturması için içler dışlar çarpımı eşit olması lazım
10×20=12×15
200≠180 olduğu için orantı oluşturmaz.
Not: Orantıda içler ve dışlar kendi arasında yer değiştirebilir.
Örnek: \dfrac{20}{16} = \dfrac{5}{4} orantısında
✅ İçleri yer değiştirirsek
\dfrac{20}{5} = \dfrac{16}{4} 👉 orantı bozulmaz.
✅ Dışları yer değiştirirsek
\dfrac{4}{16} = \dfrac{5}{20} 👉 orantı bozulmaz.

