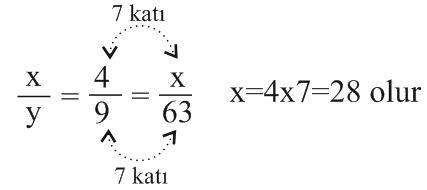Doğru Orantı Nedir ?

[alert color=”warning”]Kazanım: Doğru orantılı iki çokluk arasındaki ilişkiyi ifade eder. [/alert]

[alert color=”primary”]Bilgi: İki çokluktan biri artarken diğeri de aynı oranda artıyorsa ya da biri azalırken diğeri de aynı oranda azalıyorsa bu çokluklar doğru orantılıdır. [/alert]

Doğru orantıya örnek verecek olursak:

✅ Bir pasta tarifinde 4 bardak una 2 bardak süt katılmaktadır.Buna göre 12 bardak una 6 bardak süt katılılır.Dikkat ederseniz un miktarı 3 katına çıktığında süt miktarıda 3 katına çıkmıştır.Burada un miktarı ile süt miktarı doğru orantılıdır.

✅ Bir fotokopi makinesi 4 dakikada 120 fotokopi çekmektedir.Buna göre bu makine 8 dakikada 240 fotokopi çeker.Süre 2 katına çıktığında fotokopi sayısı da 2 katına çıkmaktadır. Burada süre ile fotokopi miktarı arasında doğru orantılı bir ilişki vardır.

Örnek: 2 ekmek 3 TL ise 8 ekmek 12 TL’dir.Ekmek ile Fiyatı arasındaki ilişkiyi inceleyelim.

✅ Ekmek adedi 4 katına çıktığında Fiyatıda 4 katına çıkmıştır.

✅ Ekmek ile fiyatı aynı oranda artmıştır.

✅ Bu yüzden ekmek ile fiyatı arasında doğru orantılı ilişki vardır.

[alert color=”danger”]Not: Çoklukların ikisi de aynı oranda artmalı veya aynı oranda azalmalıdır. Yani biri 4 katına çıktığında diğerinin de 4 katına çıkması gerek.Örneğin çocukken yaşımız arttıkça boyumuzda artar ama yaşımız 3 katına çıktığında boyumuz 3 katına çıkmaz. Bu yüzden yaşımız ile boyumuz arasında doğru orantı yoktur.[/alert]

[alert color=”warning”]Kazanım: Doğru orantılı iki çokluğa ait orantı sabitini belirler ve yorumlar. [/alert]

[alert color=”primary”]Bilgi: Doğru orantılı çoklukların birbirine bölümü sabit bir sayıya eşittir. Bu sayıya orantı sabiti denir. x ve y doğru orantılı iki çokluk k sabit bir sayı olmak üzere \( \dfrac{x}{y}=k \) ve x=y×k [/alert]

Örnek: x ve y sayıları doğru orantılıdır. x= 28 iken y=12 olduğuna göre y=3 olduğunda x kaç olur.?

Çözüm: x= 28 iken y=12 ise

\( \dfrac{x}{y}=k \)

⇒\( \dfrac{28}{12}=k \)

orantı sabitini buluruz.

✅ y=3 olduğunda x değerini bulalım

\( \dfrac{x}{y}=k \)

⇒ \( \dfrac{x}{3}=\dfrac{28}{12} \)

✅ içler dışlar çarpımı yaparız.

\( 12×x=28×3 \)

⇒\( 12×x=84 \)

⇒ x=84÷12

⇒ x=7 olur.

Örnek: Saatteki hızı 70 km/sa olan bir aracın zamanla gittiği mesafe aşağıdaki tabloda verilmiştir.

✅ Yukarıdaki tabloda zaman ile mesafe arasındaki ilişki doğru orantılıdır.

✅ Mesafenin zamana oranı sabittir.

\( \dfrac{mesafe}{zaman} \)

\[ \frac{70}{1}=\frac{140}{2}=\frac{210}{3}=\frac{280}{4}\]

orantı sabiti 70’dir.

[alert color=”danger”]Not: Eğer iki çokluk orantılıdır deniliyorsa bu iki çokluğun doğru orantılı olduğunu anlamalıyız. [/alert]

Örnek: Bir üçgenin iç açıları 5,6 ve 7 ile orantılıdır.Buna göre bu üçgenin en küçük iç açısı kaç derecedir?

Çözüm:

✅ 5,6 ve 7 ile orantılı ifadesinden 5,6 ve 7 ile doğru orantılı olduğunu anlamalıyız.

✅ Doğru orantılı olduğu için 5,6 ve 7’yi aynı oranda arttırabiliriz.

✅ 10 katını alırsak 50,60 ve 70 olur.

✅ Toplamı 180 olur ve üçgen olma şartını sağlar.

✅ En küçük açı 50 derece olur.

[alert color=”danger”]Not: Bir doğru orantıda paylar birbirinin kaç katı ise paydalarda birbirinin aynı katı olmak zorundadır. [/alert]

Örnek: x ve y doğru orantılıdır. x=4 iken y= 9’dur.Buna göre y=63 iken x kaçtır?

Çözüm: