Temel Geometrik Kavramlar

Kazanım : Doğru, doğru parçası, ışını açıklar ve sembolle gösterir.

TEMEL GEOMETRİK KAVRAMLAR

Doğru nedir?

Bilgi: Her iki ucundan sonsuza kadar uzayan düz çizgiye doğru denir.

Doğrunun Özellikleri

✅ Doğrunun başlangıç ve bitiş noktası yoktur. Bundan dolayı her iki ucuna ok konulur.

✅ Tek boyutludur.

✅ Doğrunun genişliği yoktur sadece uzunluğu vardır ama ölçülemez.

✅ Bir noktadan sonsuz doğru geçer.

✅ İki noktadan tek bir doğru geçer.

Doğru Parçası Nedir?

Bilgi: Her iki ucundan sınırlı düz çizgiye doğru parçası denir.

Doğru Parçasının Özellikleri

✅ Doğru parçasının başlangıcı ve sonu vardır.

✅ Genişliği yoktur ,uzunluğu vardır .Ölçülebilir.

✅ Tek boyutludur.

Işın Nedir?

Bilgi: Bir ucu sınırlı diğer ucu sonsuza giden düz çizgiye ışın denir.

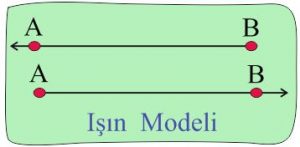
Işının Özellikleri

✅ Işının başlangıcı var ama sonu yoktur..

✅ Genişliği yoktur ,uzunluğu vardır .Ölçülemez.

✅ Tek boyutludur.

İki Doğrunun Birbirlerine Göre Durumları

Kesişen Doğrular

Bilgi: İki doğru birbirini tek bir noktada kesiyor ise bu doğrulara kesişen doğrular denir.

✅ Kesişen doğru modeli

Yukarıda verilen ”m” ve ”n” doğruları A  noktasından birbirini kesmiştir.

m ve doğruları A noktası dışında başka noktada kesişmediği için m ve n doğruları kesişen doğrulardır.

Dik Kesişen Doğrular

Bilgi: Aynı düzlemde birbirini 90 derecelik açıyla kesen doğrulara dik doğrular denir. Dik doğrular  ” ⊥ ”  sembolü ile gösterilir. Dik doğrular aynı zamanda kesişen doğrulardır.

✅ Dik kesişen doğru modeli

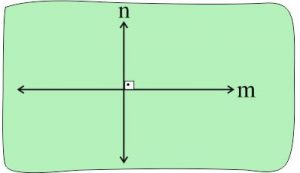
Yukarıda ”m” ve ”n” doğrusu 90 derecelik açı ile kesişmiştir.

”m” doğrusu  ”n” doğrusuna dik denir ve aşağıdaki gibi sembolle gösterilir.

m ⊥ n   (”m” doğrusu diktir ”n” doğrusuna  şeklinde okunur.)

Paralel Doğrular

Bilgi: Aynı düzlemde olup hiçbir noktada kesişmeyen doğrulara paralel doğrular denir. Paralel doğrular ”//” sembolü ile gösterilir.

✅ Paralel doğru modeli

Yukarıda ”m” ve ”n” doğrusu hiçbir noktada kesişmemektedir.

”m” doğrusu  ”n” doğrusuna paraleldir denir ve aşağıdaki gibi sembolle gösterilir.

m //  n  (”m” doğrusu ”n” doğrusuna  paraleldir şeklinde okunur.)

Çakışık Doğrular

Bilgi: Aynı düzlemde olup tüm noktaları ortak olan doğrulara çakışık doğrular denir.

✅ Çakışık doğru modeli

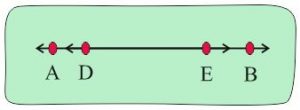
Çakışık Doğruların tüm noktaları aynı olduğu için bu iki doğruyu aynı iki doğru olarak düşünebiliriz.

Not: Paralel doğruların arasındaki mesafeyi sıfıra indirdiğimizde çakışık doğrular olur. Çakışık doğrular birbirine paralel değildir.

Temel Geometrik Kavramlar Test

Temel geometrik kavramlar eşleştirme etkinliğini yaparak konuyu daha iyi kavrayabilirsiniz. Etkinlik açılmazsa sayfayı yenileyiniz.

🔻 Diğer konulara hızlı geçiş 🚀

⏪ Önceki Konu	Sonraki Konu ⏩
	Bir Noktanın Diğer Bir Noktaya Göre Konumu