Tam Sayılarla Çarpma ve Bölme İşlemleri Konu Anlatımı – 7.Sınıf

Kazanım: Tam sayılarla çarpma ve bölme işlemlerini yapar.

Tam Sayılarla Çarpma ve Bölme

Tam Sayılarda Çarpma İşlemi

Tam sayılarda çarpma işlemi yaparken önce işaretler sonra sayılar çarpılır. İşaretlerin çarpımını aynı işaretli ve zıt işaretli olmak üzere iki başlıkta inceleyelim.

Bilgi: Aynı işaretli iki tam sayının çarpımı pozitif bir tam sayıdır.

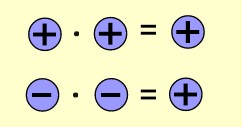
Örneğin (-7)·(-3) çarpma işlemini yaparken önce işaretleri çarparız. Sonra sayıları çarparız.

İşaretlerin çarpımı ➖·➖=➕

Sayıları çarpımı 7·3=21

Sonuç +21 olarak bulunur.

Örnek: (-8)·(-5)=❓işleminin sonucu bulalım.

Çözüm:

🤓 Tam sayılarda çarpma işlemi yaparken önce işaretler sonra sayılar çarpılır..

İşaretlerin çarpımı ➖·➖=➕

Sayıları çarpımı 8·5=40

Sonuç +40 olarak bulunur.

Bilgi: Zıt işaretli iki tam sayının çarpımı negatif bir tam sayıdır.

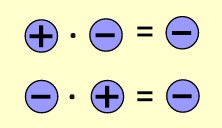
Örneğin (+6)·(-4) çarpma işlemini yaparken önce işaretleri çarparız. Sonra sayıları çarparız.

İşaretlerin çarpımı ➕·➖=➖

Sayıları çarpımı 6·4=24

Sonuç -24 olarak bulunur.

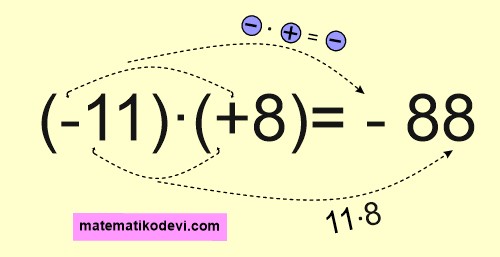
Örnek: (-11)·(+8)=❓işleminin sonucu bulalım.

Çözüm:

🤓 Tam sayılarda çarpma işlemi yaparken önce işaretler sonra sayılar çarpılır..

İşaretlerin çarpımı ➖·➕=➖

Sayıları çarpımı 11·8=88

Sonuç -88 olarak bulunur.

Tam Sayılarda Çarpma İşleminin Sayma Pulları İle Gösterimi

Tam sayılarda çarpma işleminde ilk sayıya 1.çarpan ikinci sayıya 2.çarpan denildiğini önceki senelerde öğrenmiştik.

Sayma pulları ile çarpma işlemini modellerken 1.çarpan grup sayısını , 2.çarpan grup içindeki pul sayısını gösterir. Sayma pulları ile çarpma işleminin modellemesini 1. çarpanın pozitif olma ve negatif olma durumuna göre 2 başlıkta inceleyelim.

Bilgi:1.çarpanın pozitif olduğu durumlarda birinci çarpanın değeri kadar grup oluşturup grupların içine ikinci çarpan kadar pul ekleriz.

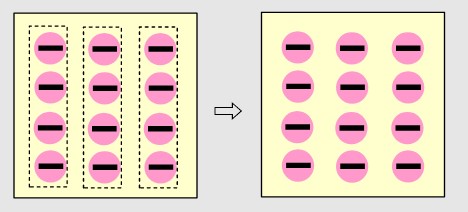
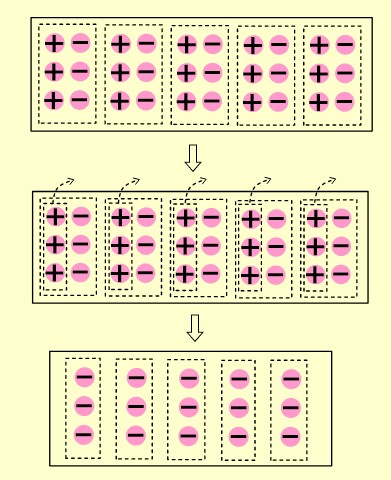
Örneğin (+3)·(-4) çarpma işlemini sayma pulu ile göstermek için

➡️ 1.çarpan 3 olduğu için 3 tane grup oluştururuz.

➡️ 2.çarpan (-4) olduğu için her grubun içinde 4 tane eksi pulu ekleriz.

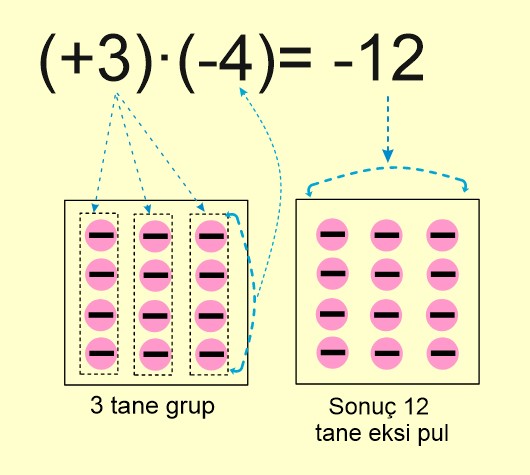
➡️ (+3)·(-4) çarpma işlemini sayma pulu ile gösterimi aşağıdaki gibidir.

Bilgi: Birinci çarpanın negatif olduğu durumlarda birinci çarpanın değeri kadar grup oluşturup ikinci çarpan kadar grupların içine sıfır çifti ekleriz. Sonra ikinci çarpan kadar pulu grupların içinden çıkarırız. Kalan pulları sonuç olarak gösteririz.

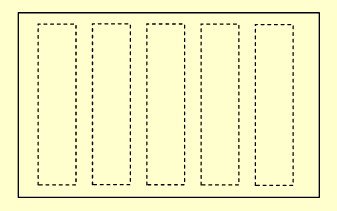
Örneğin (-5)·(+3) çarpma işlemini sayma pulu ile göstermek için

➡️ 1.çarpan (-5) olduğu için 5 tane grup oluştururuz.

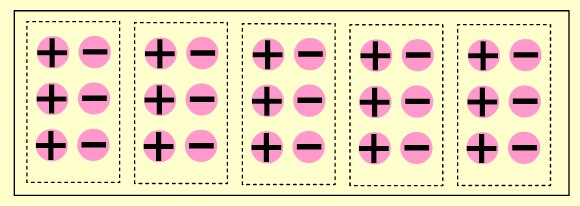
➡️ 2.çarpan (+3) olduğu için her grubun içinde 3 tane sıfır çifti ekleriz.

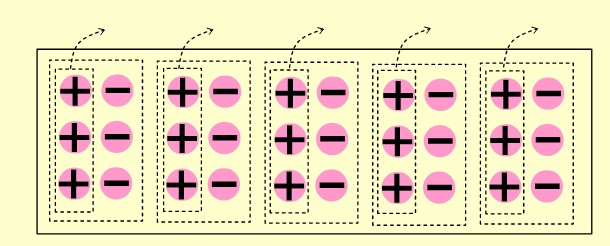
➡️ 1.çarpan eksi olduğu için grupların içerisinden 2. çarpan kadar pulu (3 tane artı pulu) çıkarırız.

➡️ Kalan pulları sonuç olarak gösteririz.

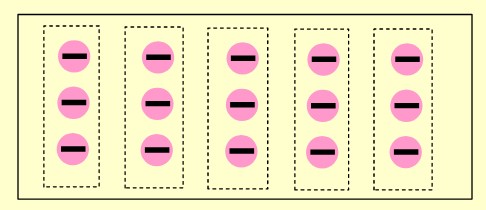
➡️ (-5)·(+3) çarpma işlemini sayma pulu ile gösterimi aşağıdaki gibidir.

Tam Sayılarda Çarpma İşleminin Sayı doğrusunda Gösterimi

Tam sayılarda çarpma işlemini sayı doğrusunda göstermek için çarpmanın ne anlama geldiğini bilmemiz gerekir.

Örneğin (+4)·(-3) demek 4 tane (-3)’ün toplamı demektir.

Yani (+4)·(-3) işlemini (-3)+(-3)+(-3)+(-3) şeklinde gösterebiliriz.

O zaman (+4)·(-3) işlemini sayı doğrusunda gösterirken 4 defa eksi yönde 3 adım gidecem.

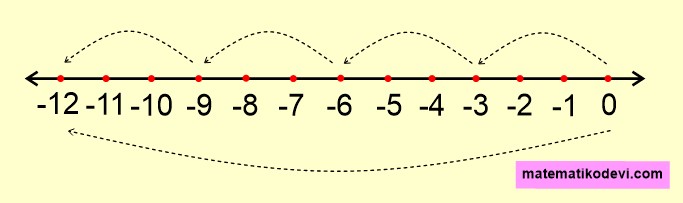
Bilgi: Birinci çarpanın ➖ ikinci çarpanın ➕ olduğu durumlarda birinci çarpan ile ikinci çarpanın işaretlerini yer değiştiririz. İşaretlerini değiştirdiğimiz işlemi sayı doğrusunda gösteririz. Örneğin (-4)·(+3) işlemini sayı doğrusunda göstermek yerine (+4)·(-3) işlemini sayı doğrusunda gösteririz.

Yani (-4)·(+3) işleminin sayı doğrusunda gösterimi aşağıdaki gibidir.

Bilgi: Birinci çarpanın ➖ ikinci çarpanın ➖ olduğu durumlarda Birinci çarpanın işaretini ➕ ikinci çarpanın işaretini ➕ yaparız. İşaretlerini değiştirdiğimiz işlemi sayı doğrusunda gösteririz. Örneğin (-4)·(-3) işlemini sayı doğrusunda göstermek yerine (+4)·(+3) işlemini sayı doğrusunda gösteririz.

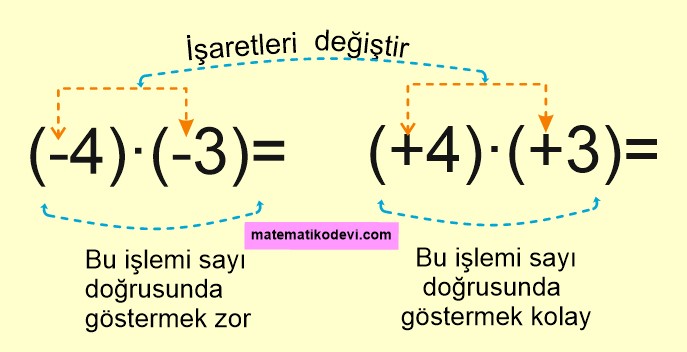
Yani (-4)·(-3) işleminin sayı doğrusunda gösterimi aşağıdaki gibidir.

Çarpma İşleminin Özellikleri

Çarpma İşleminin Değişme Özelliği

Bilgi: Çarpma işleminde çarpılan sayıların yeri değişse de işlemin sonucu değişmez. Bu duruma tam sayılarda çarpma işleminin değişme özelliği denir.

(+6)·(-4) işleminin sonucu -24

(-4)·(+6) işleminin sonucu da -24 ‘dür.

Yukarıdaki iki işlemi incelediğimizde çarpma işleminde sayıların yeri değişse de sonucun değişmediğini görürüz.

Birleşme Özelliği

Bilgi: Üç veya daha fazla tam sayı ile çarpma işlemi yaparken çarptığımız sayıları farklı şekilde gruplandırarak çarpsak da sonuç değişmez. Bu duruma Tam Sayılarda Çarpma İşleminin Birleşme Özelliği denir.

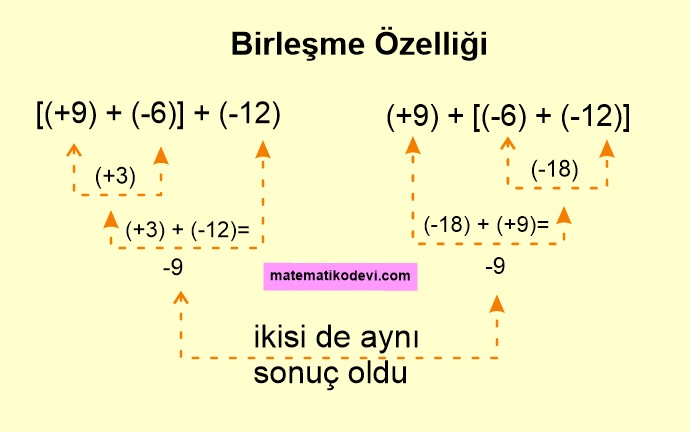
Örneğin [(+4)·(-5)]·(-2) işlemi ile (+4)·[(-5)·(-2)] işleminin sonuçlarını karşılaştıralım.

🤓 [(+4)·(-5)]·(-2) Bu işlemde köşeli parantez kullanarak ilk iki sayıyı gruplandırmış.

🤓 (+4)·[(-5)·(-2)] Bu işlemde köşeli parantez kullanarak son iki sayıyı gruplandırmış.

➡️[(+4)·(-5)]·(-2) işleminde önce köşeli parantezden işleme başlanır.

(+4)·(-5) = -20 olarak bulunur. Sonra bulduğumuz sonucu (-2) ile çarparız.

(-20)·(-2)= +40

➡️ (+4)·[(-5)·(-2)] işleminde önce köşeli parantezden işleme başlanır.

(-5)·(-2)= +10 olarak bulunur. Sonra bulduğumuz sonucu (+4) ile çarparız.

(+10)·(+4)=+40

🤓 [(+4)·(-5)]·(-2) işlemi ile (+4)·[(-5)·(-2)] işleminin sonuçları aynı çıktı.

Bu durumu [(+4)·(-5)]·(-2) = (+4)·[(-5)·(-2)] şeklinde gösterip yapılan bu işlemede tam sayılarda çarpma işleminin birleşme özelliği denir.

Çarpma İşleminin Toplama ve Çıkarma Üzerine Dağılma Özelliği

Çarpma işlemini toplama ve çıkarma işlemi üzerine dağıtabiliriz.

➡️ Çarpmanın işleminin toplama üzerine dağılma Özelliği 

Örneğin

(− 4) · ( (+7) + (-5) ) işleminde parantez dışındaki çarpan olan −4’ü içerideki sayılarla sırayla çarparız. Daha sonra içerideki işlem toplama olduğu için çıkan sonuçları toplarız.

(− 4) · ( (+7) + (-5) )

= ((− 4) · (+7)) + ((− 4) · (-5))

= (− 28) + (+20)

= − 8

Bu işleme çarpma işleminin toplama üzerine dağılma özelliğini denir.

➡️ Çarpmanın işleminin çıkarma üzerine dağılma Özelliği 

Örneğin

(+ 6) · ( (-7) – (+5) ) işleminde parantez dışındaki çarpan olan + 6’yı içerideki sayılarla sırayla çarparız. Daha sonra içerideki işlem çıkarma olduğu için çıkan sonuçları çıkarırız.

(+ 6) · ( (-7) – (+5) )

= ((+ 6) · (-7) + ((+ 6) · (+5))

= (− 42) + (+30)

= − 12

Bu işleme çarpma işleminin çıkarma üzerine dağılma özelliğini denir.

➡️ Çarpmanın toplama ve çıkarma işlemi üzerinde dağılma özelliği zihinden işlem yapmamızı  kolaylaştırır.

Örneğin;

12 · 97 işlemini ele alalım. 97’nin 100’den üç eksik olduğunu biliyoruz.

12 · ( 100 − 3) şimdi çarpmayı çıkarma üzerine dağıtalım.

= 12 · 100 − 12 · 2

= 1200 − 36

= 1164 olarak buluruz.

Çarpma İşleminin Etkisiz Elamanı (Birim Eleman)

Bilgi: Çarpma işleminde çarpım yaparken sonucu değiştirmeyen sayıya etkisiz (birim) eleman denir. Çarpma işleminde herhangi bir sayıyı 1 ile çarptığımızda sonuç değişmez. Bu yüzden çarpma işleminin etkisiz (birim) elemanı 1’dir.

(− 45) · 1 = − 45

(+56) · 1 = +56

(− 27) · 1 = − 27

Çarpma İşleminin Yutan Elamanı

Bilgi: Hangi sayıyla çarpılırsa çarpılsın sonuç yine kendisi olan sayıya çarpma işleminde yutan eleman denir. Çarpma işleminde her sayının 0 (sıfır) ile çarpımı sıfıra yani kendisine eşittir. Bu yüzden çarpma işleminin yutan elemanı 0’dır.

(− 45) · 0 = 0

(+25) · 0 = 0

Tam Sayılarda Bölme İşlemi

Tam sayılarda bölme işlemi yaparken önce işaretler sonra sayılar bölünür. İşaretlerin bölümünü aynı işaretli ve zıt işaretli olmak üzere iki başlıkta inceleyelim.

Bilgi: Aynı işaretli iki tam sayının bölümü pozitif bir tam sayıdır.

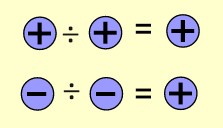
Örneğin (-12)÷(-3) bölme işlemini yaparken önce işaretleri böleriz. Sonra sayıları böleriz.

İşaretlerin bölümü ➖÷➖=➕

Sayıların bölümü 12÷3=4

Sonuç +4 olarak bulunur.

Örnek: (+36)÷(+3) işleminin sonucunu bulunuz❓

🤓 Tam sayılarda bölme işlemi yaparken önce işaretler sonra sayılar bölünür.

İşaretlerin bölümü ➖÷➖=➕

Sayıları bölümü 36÷3=12

Sonuç +12 olarak bulunur.

Bilgi: Zıt işaretli iki tam sayının bölümü negatif bir tam sayıdır.

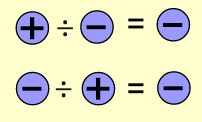
Örneğin (-60)÷(+12) bölme işlemini yaparken önce işaretleri böleriz. Sonra sayıları böleriz.

İşaretlerin bölümü ➖÷➕=➖

Sayıların bölümü 60÷12=5

Sonuç – 5 olarak bulunur.

Örnek: (+48)÷(-8) işleminin sonucunu bulunuz❓

🤓 Tam sayılarda bölme işlemi yaparken önce işaretler sonra sayılar bölünür.

İşaretlerin bölümü ➕÷➖=➖

Sayıları bölümü 48÷8=6

Sonuç – 8 olarak bulunur.

Tam Sayılarda Bölme İşleminin Sayma Pulları İle Gösterimi

Bölme işleminde 1.sayı bölünen sayı 2.sayı bölen sayı olduğunu önceki senelerde öğrenmiştik. Tam sayılarda bölme işlemini sayma pulları ile gösterirken bölen sayının pozitif ve negatif olma durumuna göre iki başlıkta inceleyelim.

➡️ Bölen sayı pozitif ise ;

• Bölünen sayı kadar pul oluştururuz.
• Oluşturduğumuz pulları bölen sayı kadar gruplara ayırırız.
• Ayırdığımız gruplardan bir tanesi sonuç olarak yazarız.

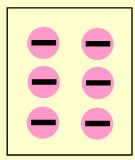
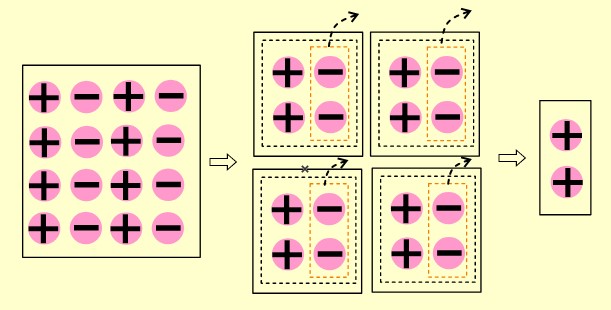
Örneğin (-6)÷(+3) işlemini modellerken

👉 Bölünen sayı kadar pul oluştururuz.

🤓 Bölünen sayı -6 olduğu için 6 tane pulu oluştururuz.

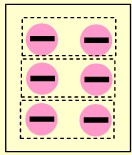
👉 Oluşturduğumuz pulları bölen sayı kadar gruplara ayırırız.

🤓 Bölen sayı 3 olduğu için (-6) ‘yı 3 gruba ayırırız.

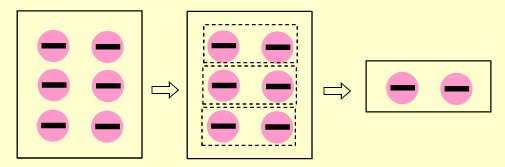
👉 Ayırdığımız gruplardan bir tanesi sonuç olarak yazarız.

👉 (-6)÷(+3) işleminin modellemesi aşağıdaki gibidir.

➡️ Bölen sayı negatif ise ;

• Bölünen sayı kadar sıfır çifti () oluştururuz.
• Oluşturduğumuz pulları bölen sayı kadar gruplara ayırırız. Oluşturduğumuz gruplardan bölen sayının işareti olan pulları çıkarırız.
• Ayırdığımız gruplardan bir tanesi sonuç olarak yazarız.

Örneğin; (-8)÷(-4) işlemini modellerken

👉 Bölünen sayı kadar sıfır çifti () oluştururuz.

🤓 Bölünen sayı (-8) olduğu için 8 tane sıfır çifti () ekleriz.

👉 Oluşturduğumuz pulları bölen sayı kadar gruplara ayırırız. Oluşturduğumuz gruplardan bölen sayının işareti olan pulları çıkarırız.

🤓 Bölen sayı 4 olduğu için 4 gruba böleriz. Bölen sayının işareti ➖ olduğu için gruplardan ➖ işaretlerini çıkarırız.

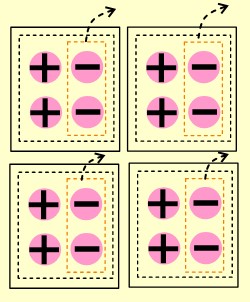
👉 Ayırdığımız gruplardan bir tanesi sonuç olarak yazarız.

🤓 Gruplardan pulları çıkarınca her grupta 2 tane artı pulu ( ) kalır.

👉 (-8)÷(-4) işleminin modellemesi aşağıdaki gibidir.

Tam Sayılarda Bölme İşleminin Sayı Doğrusunda Gösterimi

Bilgi: Tam sayılarda bölme işlemini sayı doğrusunda gösterirken ; bölünen sayıdan başlayıp sıfıra doğru eşit adımlarla bölen sayı kadar adımda ilerleriz.

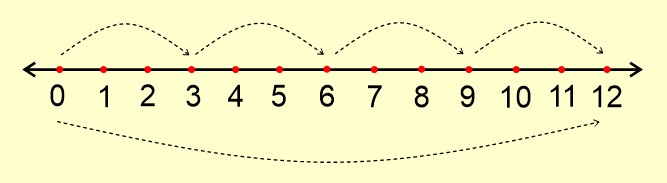
Örneğin (-12)÷(+4) işlemini sayı doğrusunda gösterirken (-12)’den başlayıp 0’a doğru 4 eşit adımda ilerleriz.

Yani (-12)÷(+4) işleminin sayı doğrusunda gösterimi

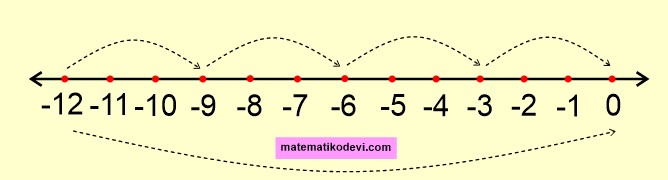
Her adımdaki sayı miktarı bize sonucu gösterir. Her adımda 3 sayı var ve yönümüz sola doğru olduğu için sonuç (-3) olur.

Not: Bölen sayının negatif olduğu durumlarda bölen sayıyı pozitif yapıp sayı doğrusunda gösteririz.

• (-12)÷(-4) işlemini sayı doğrusunda göstermek yerine (+12)÷(+4) işlemini sayı doğrusunda gösteririz.

• (+12)÷(-4) işlemini sayı doğrusunda göstermek yerine (-12)÷(+4) işlemini sayı doğrusunda gösteririz.

tam sayılarda çarpma ve bölme işlemi test

7.Sınıf Matematik İçerikleri : https://www.matematikodevi.com/7-sinif-matematik/

Instagram adresi : https://www.instagram.com/matara_33/

🔻 Diğer konulara hızlı geçiş 🚀

⏪ Önceki Konu	Sonraki Konu ⏩
Toplama İşleminin Özellikleri	Tam Sayıların Kuvveti