Matematik Terimleri ve Anlamları

Matematik, hayatımızın birçok alanında önemli bir yere sahip olan bir bilim dalıdır. Doğal olayların analizi, bilim araştırmaları ve teknoloji gibi alanlarda matematiksel hesaplamalar yapılmaktadır. Bu makalede, matematik terimleri ve anlamlarını ele alacağız.

Matematik Terimleri

Sayılar

Matematik terimlerine sayılar ile başlayalım. Matematikte sayılar, temel bir kavramdır ve birçok matematiksel işlem için gereklidir. Tam sayılar, sayıların en temel şeklidir ve negatif, pozitif ve sıfırı içerirler. Doğal sayılar ise sıfır ve pozitif tamsayıları ifade ederler. Ondalık sayılar, tam sayıların ardından virgülle ayrılan sayılar olarak tanımlanırlar. Kesirler de bir bölümün paydasına oranını veren matematiksel bir ifade olarak kullanılırlar. Rasyonel sayılar, kesirlerin oranı olarak ifade edilen sayılar, irrasyonel sayılar ise rasyonel olmayan, sayıların kesirle ifade edilemeyen türleridir.

Matematiksel işlem ve problemleri çözerken, bu temel sayı kavramlarına hakim olmak önemlidir.

Tam Sayılar

Tam sayılar, pozitif ve negatif tüm sayıları içeren bir sayı kümesidir. Bu sayılar, doğal sayıların yanı sıra sıfırı da içerir. Matematiksel olarak, Z sembolü ile gösterilir. Tam sayılar, matematiksel işlemler için kullanıldığı gibi, gerçek dünya problemlerinin çözümünde de önemli bir rol oynarlar. Örneğin, para miktarları ve yaş gibi gerçek dünya verileri tam sayılarla ifade edilebilir. Tam sayılarla ilgili temel matematiksel kavramlar arasında zıt sayılar, mutlak değerler ve aralıklar yer alır. 6. Sınıf Tam sayılar konu anlatımına buraya tıklayıp ulaşabilirsiniz.

• Zıt Sayılar: Pozitif ve negatif sayılar başka bir pozitif veya negatif sayıya zıt sayı denir. Örneğin, 3 ve -3 birbirinin zıt sayılarıdır.
• Mutlak Değer: Bir sayının mutlak değeri, sayının sıfırdan uzaklık mesafesidir. Mutlak değer genellikle dikey çizgi ile gösterilir. Örneğin, |-2| = 2 ve |4| = 4.
• Aralıklar: Aralık, bir sayı kümesini ifade eden bir matematiksel terimdir. Örneğin, [-3,3] aralığı, -3 ile 3 arasındaki tüm tam sayıları temsil eder.

Doğal Sayılar

Doğal sayılar, temel olarak, sıfırdan başlayarak tüm pozitif tamsayıları içeren bir sayı kümesidir. Bu sayılara matematikte genellikle “N” harfi ile işaret edilir. Örneğin 0,1, 2, 3, 4, 5, 6 gibi sayılar doğal sayılardır. Doğal sayılar, temel matematik işlemleri olan toplama, çıkarma, çarpma ve bölme için kullanılır. Aynı zamanda diğer matematik dallarında da kullanılmaktadır. Tablolar veya listeler kullanılarak, doğal sayıların özellikleri ve uygulamaları hakkında daha fazla bilgi edinmek mümkündür.

Rasyonel Sayılar:

➡️ a ve b tam sayıları olmak üzere a/b şeklinde yazılabilen sayılara rasyonel sayılar denir.

➡️ Rasyonel sayılar Q ile sembolü ile gösterilir.

➡️ Rasyonel sayıların içerisinde sayma sayıları, doğal sayılar, devirli ondalık sayılar, tam kare sayılar, tam sayılar dahildir.

Sayma sayıları :

➡️ 1’den başlayıp sonsuza kadar devam eden sayılara sayma sayıları denir.

➡️ N+ ile gösterilir.

Tam kare sayılar :

➡️ Kök içerisine alındığında dışarıya tam olarak çıkabilen sayılar veya bir sayının karesi şeklinde yazılabilen sayılara tam kare sayılar denir.

Örneğin 1,4,9,16 gibi sayılar tam kare sayılardır.

1 = 1²

4 = 2²

9 = 3²

16 = 4²

Devirli ondalık sayılar :

➡️ Ondalık sayılarda virgülden sonra aynı rakam veya sayıların tekrar etmesine devirli ondalık sayılar denir.

Örneğin 1,44444444 sayısı devirli ondalık sayıdır.

İRRASYONEL SAYILAR :

➡️ a ve b tam sayılar olmak üzere a/b şeklinde yazılamayan sayılara irrasyonel sayılar denir.

➡️ I sembolü ile gösterilir.

➡️ Karekök Dışına Çıkamayan Sayılar

• 2√7
• √3

➡️ Virgülden Sonra Düzensiz İlerleyen Sayılar

• 3,142857128436…… π sayısı
• 2,718285217824…….. e sayısı

GERÇEK (REEEL) SAYILAR :

➡️ Rasyonel sayılar ile irrasyonel sayıların birleşimine gerçek (reel) sayılar denir.

➡️ R = I U Q

Kesirler

Kesirler, bir bölümün paydasına oranını veren matematiksel bir ifadedir. Genellikle iki sayı arasında bir çizgi ile ayrılırlar ve a/b şeklinde yazılırlar.

Kesirler matematikte önemli bir konudur. Pay ise bölünen nesnenin bir parçasını ifade eder. Pay ve payda arasındaki ilişki kesrin değerini belirler. Bu nedenle, kesirlerin önemli bir matematiksel kavram olduğu söylenebilir.

• Bir kesrin değeri payın paydaya bölünmesi ile bulunur.
• Payda sıfır olamaz.
• Bir tam sayı bir kesir olarak yazılabilir.

Matematik Terimleri	Anlamı
Kesir	Bir bölümün paydasına oranını veren matematiksel bir ifade
Pay	Bölünen nesnenin bir parçasını ifade eder
Payda	Eşit parçalara bölünmüş bir nesneyi temsil eder

Kesirler; basit kesir, bileşik kesir ve tam sayılı kesir olmak üzere 3’e ayrılır.

Basit Kesir : Payı paydasından küçük olan kesirlere basit kesir denir.

Bileşik Kesir : Payı paydasına eşit veya büyük olan kesirlere bileşik kesir denir.

Tam Sayılı Kesir : Bir sayma sayısı ve bir basit kesir ile yazılmış dolan kesirlere tam sayılı kesirler denir.

Örüntü

Belirli bir kuralı takip eden şekil veya sayı dizileri birer örüntüdür. Örüntüler sayı örüntüsü ve şekil örüntüsü olmak üzere ikiye ayrılır.

Sayı örüntüsü: Belirli bir kurala göre ilerleyen sayı dizisine denir

Örneğin 1, 5, 9, 13, 17, 21, … sayıları 4’er artarak ilerlemiş. Bu yüzden bu sayı dizisi sayı örüntüsüdür.

Şekil Örüntüsü: Belirli bir kuralla göre ilerleyen şekillere şekil örüntüsü denir.

Örneğin yukarıdaki şekil her adımda 4 kare artarak ilerlemiştir. Bu yüzden yukarıdaki şekil örüntüsüdür.

Terim: Bir sayı örüntüsünü oluşturan her sayıya terim denir.

2, 7, 12, 17, 22, 27, …

Örneğin yukarıdaki örüntünün ilk terimi 2’dir ve 5. terimi 22’dir.

“n” harfi, örüntüdeki sayıların sırasını veya yerini belirten işaret, sembol veya notasyondur. Bu yüzden n’ye örüntünün n. sayısı, temsilci sayısı veya genel sayısı denir.
Bir sayı örüntüsünde n. sıradaki sayının n değişkeni cinsinden ifadesine örüntünün kuralı denir.

Örüntünün kuralında istenilen adımdaki sayıyı bulmak için n yerine istenilen adım sayısı yazılarak adımdaki sayı bulunur.

Örneğin  3, 6, 9, 12, 15, diye devam eden örüntünün kuralı 2.n’dir.

Bu örüntüde 15. terimi bulmak için örüntünün kuralındaki n yerine 15 yazarız.

2.n = 2.15 = 30 buluruz. Örüntünün 15. terimi 30’dur.

8n+3 örüntüsünün 7. terimini bulmak için n yerine 7 yazarız:

8.7 + 3 = 56 + 3 = 59

Örüntünün Kuralını Bulma

Örüntü kuralını bulmak için sayılar arasındaki ilişkiyi bulmamız gerekir.

Örneğin 5, 9, 15, 24, 33, ………

1. Terim ➡️ 5

2. Terim ➡️ 9

3. Terim ➡️ 13

…

n. Terim ➡️ 4n+1 (genel terim)

Bu kuralı şöyle bulduk:

Örüntüyü incelersek her adımda 4’er 4’er artıyor. O yüzden n’i 4 ile çarparız. (4n)

Daha sonra örüntünün ilk terimi 5’miş. Yani kuralda n yerine 1 yazınca sonuç 5 çıkacak. 4n kuralında 4 çıkıyor. O yüzden 1 ekliyoruz. (4n+1)

Kontrol edebiliriz. 4n+1 kuralında 3.terimin 13 çıkması lazım. 4.3+1=13

Yüzdeler

Paydası 100 olan kesirleri % sembolü ile gösterilmesidir.

Örneğin 33/100 kesrini % 33 şeklinde gösterip yüzde otuz üç diye okuruz.

Yüzde şeklinde verilen ifadeleri karşılaştırırken yüzde sembolünü görmeden direk sayıları karşılaştırabiliriz.

Örneğin % 45 ifadesi % 40 ifadesinden büyüktür. Çünkü 45 sayısı 40 sayısından büyüktür.

Bir sayının belirli bir yüzdesini bulurken önce yüzdeyi kesre çeviririz. Sonra sayıyı pay ile çarpıp paydaya böleriz.

Örneğin 200 sayısının % 40 ‘nı bulurken 200’ü 40 ile çarpıp 100’e böleriz.

200×40=8000

8000:100 = 80

200’ün %40’ı 80 yapar.

Bir çokluğu diğer bir çokluğun yüzdesi olarak yazarken ilk söylenen sayıyı paya ikinci söylenen sayıyı paydaya yazarız. Sonra oluşan kesri paydası 100 olacak şekilde sadeleştirir veya genişletiriz.

Örneğin 36 sayısı 100 sayısının % kaçıdır?

✅ ilk söylenen sayı paya ➡️ 36 (pay)

✅ İkinci söylenen sayı paydaya ➡️ 100 (paydaya)

✅ 36/100

✅ % 36

Bir çokluğu belirli bir yüzde ile arttırmayı veya azaltmayı kısa yoldan aşağıdaki örneklerdeki gibi yapabiliriz.

✅ Bir sayıyı % 12 arttırmak için bu sayıyı 1,12 ile çarparız.  (%100+%12=%112)

✅ Bir sayıyı % 14 azaltmak için bu sayıyı 0,86 ile çarparız.  (%100-%14=%86)

✅ Bir sayıyı % 28 arttırmak için bu sayıyı 1,28 ile çarparız. (%100+%28=%128)

✅ Bir sayıyı % 30 azaltmak için bu sayıyı 0,7 ile çarparız.  (%100-%30=%70)

Kümeler

İyi tanımlanmış birbirinden farklı nesneler topluluğuna küme denir. Kümeler A, B, C, D gibi büyük harflerle isimlendirilir.

”bazı” , ”güzel” , ”çalışkan” , ”uzun boylu” gibi kişiden kişiye (öznel) değişen ifadeler küme belirtmez.

Aşağıdaki ifadeler küme belirtir.

• Niğde’nin ilçeleri
• ” MATEMATİK ÖDEVİ ” kelimesinin harfleri
• 8 ile 25 arasındaki doğal sayılar
• Haftanın S harfi ile başlayan günleri
• Okulumuzdaki bay öğretmenler

Herkes tarafından yok diye tanımlanan ifadeler küme belirtir.

• 12 ile 13 arasındaki doğal sayılar.
• Ğ harfi ile başlayan isimler.
• Yüzen aslanlar.

Bir kümeyi oluşturan nesnelerin her birine o kümenin elemanı denir. Verilen nesnenin bir kümeye ait olduğunu elemanıdır anlamına gelen “∈” sembolü kullanır. Verilen nesnenin bir kümeye ait olduğunu elemanı değildir anlamına gelen ”∉” sembolü kullanılır.

Örneğin; A kümesi aşağıdaki elemanlardan oluşsun.

A = {a, b, c} ise

a∈A 👉 ”a” A kümesinin elamanıdır.

d∉A 👉 ”d” A kümesinin elamanı değildir.

 Bir kümede bulunan varlıkların sayısına eleman sayısı denir. Eleman sayısını sembolle s(A) şeklinde gösterilir.

Örneğin;

D kümesinin eleman sayısı 6 ise s(D)=6 şeklinde gösterilir.

F kümesinin eleman sayısı 7 ise s(F)=7 şeklinde gösterilir.

Kümelerin Farklı Gösterimleri

Kümeler; liste yöntemi, ortak özellik yöntemi ve Venn şeması olmak üzere üç şekilde gösterilebilir.

Kümenin elemanlarının “{ }” içerisine aralarına virgül konularak yazılmasına liste yöntemi denir.

Örneğin MATEMATİK ÖDEVİ kelimesinin harflerini liste yöntemiyle yazalım.

Kümeyi F harfiyle isimlendirecek olursak F = { M, A, T, E, İ, K, Ö, D, V }

Kümeye ait elemanların kapalı bir geometrik şekil içerisinde ve her elemanın başına bir nokta konularak gösterilmesine Venn şeması yöntemi denir.

Bir kümenin elemanlarını tanımlayan ortak özeliğin sözel bir ifade ile küme parantezi içinde yazılmasına ortak özellik yöntemi denir.

A = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 } kümesi liste yöntemi ile ifade edilmiştir. A kümesini ortak özellik yöntemi ile ifade edecek olursak A = { Rakamlar }

Elemanı olmayan kümelere boş küme denir. Boş küme ∅ ya da { } sembolü ile gösterilir.

Örneğin D = {K harfi ile başlayan günler} kümesine ait eleman olmadığı için, bu kümenin eleman sayısını s(D) = ∅ ya da s(D) = { } şeklinde ifade ederiz.

Kümelerle İşlemler

A ve B gibi iki kümenin bütün elemanlarının yazılması ile oluşan yeni kümeye, A kümesi ile B kümesinin birleşim kümesi denir. Kümelerde birleşim işlemi “U” sembolü ile gösterilir. A kümesi ile B kümesinin birleşimini ”AUB” şeklinde gösteririz.

Örneğin;

K = {a, b, c, d, e, f}

L = {1, a, 3, b} kümeleri verilmiş olsun.

K ve L kümesinin birleşim kümesini KUL = {a, b, c, d, e, f, 1, 3} şeklinde yazarız.

A ve B gibi iki kümenin ortak elemanlarının yazılması ile oluşan kümeye, bu iki kümenin kesişim kümesi denir. Kesişim işlemi “∩” sembolü ile gösterilir. A ve B kümesinin kesişim kümesini A ∩ B şeklinde gösteririz.

Örneğin;

K = {a, b, c, d, e, f}

L = {1, a, 3, b} kümeleri verilmiş olsun.

K ve L kümesinin kesişim kümesini K∩L = {a, b} şeklinde yazarız.

Uzunluk Ölçü Birimleri

• Uzunluk ölçü birimleri km – hm- dam – m – dm – cm – mm  şeklinde sıralanır.
• Bu sıralamada soldan sağa doğru giderken sayıyı her basamakta 10 ile çarparız.
• Sağdan sola doğru giderken sayıyı her basamakta 10’a böleriz.
• Sıralamayı kalıcı olması için  “KAMİLE (km) HALAM (hm) DAMDA (dam) MEHMET (m) DAYIM (dm) CAMDA (cm) MERHABA MERHABA (mm)” tekerlemesini ezberleyebilirsiniz.

Örneğin 35 metre kaç santimetredir?

Metreden santimetreye gitmek için 2 basamak sağa gideriz

Yani sayımızı 10 ile iki kere çarpacağız.

35 x 10 = 350
350 x 10 = 3500 cm

Örneğin 8400 milimetre kaç metredir?

Milimetreden metreye gitmek için 3 basamak sola gideriz.

Yani sayımızı 10’a üç kere böleceğiz.

8400 : 10 = 840
840 : 10 = 84
84 : 10 = 8,4 m

Zaman Ölçü Birimleri

Bir dakikanın altmışta biri olan zaman ölçü birimine saniye denir ve saniye kısaca sn ile gösterilir.

3 dakika kaç saniyedir bulalım.

Dakikayı saniyeye çevirirken 60 ile çarparız.
5 dakika ➔ 5 x 60 = 300 saniyedir.

480 saniye kaç dakikadır bulalım.

Saniyeyi dakikaya çevirirken 60’a böleriz.
720 saniye ➔ 720 : 60 = 12 dakikadır.

60 saniyelik zaman ölçü birimine dakika denir ve dakika kısaca dk ile gösterilir.

Dakikayı saniyeye çevirirken 60 ile çarparız.
4 dk ➔ 4 x 60 sn = 240 sn

Bir günlük sürenin yirmi dörtte birine eşit, altmış dakikalık zaman dilimine saat denir ve kısaca sa ile gösterilir.

Saati dakikaya çevirirken 60 ile çarparız..
7 sa ➔ 7 x 60 = 420 dk

Dünya’nın kendi ekseni etrafında 1 kez dönmesiyle geçen 24 saatlik süreye gün denir.

Günü saate çevirirken 24 ile çarparız.
4 gün ➔ 4 x 24 = 96 sa

Birbirini takip eden 7 günden oluşan zaman parçasına hafta denir. Bir hafta 7 gündür.

Haftayı güne çevirirken 7 ile çarparız.
5 hafta ➔ 5 x 7 = 35 gün

Yılın on iki bölümünden her birine ay denir. Matematik sorularında bir ayı 30 gün olarak hesaplarız.

Bir yılı 365 gün, 6 saatlik zamana yıl denir. Matematik sorularında bir yılı 365 gün olarak hesaplarız.

Özet olarak ;

• 1 yıl = 365 gün = 12 ay = 52 hafta
• 1 ay = 30 gün
• 1 hafta = 7 gün
• 1 gün = 24 saat
• 1 saat = 60 dakika
• 1 dakika = 60 saniye

Alan Ölçü Birimleri

• Alan ölçü birimleri km² – hm² – dam² – m² – dm² – cm² – mm² şeklinde sıralanır.
• Bu sıralamada soldan sağa doğru giderken sayıyı her basamakta 100 ile çarparız.
• Sağdan sola doğru giderken sayıyı her basamakta 100’e böleriz.

Örneğin 43 metrekare kaç santimetrekaredir?

Metrekareden santimetrekareye gitmek için 2 basamak sağa gideriz.

Yani sayımızı 100 ile iki kere çarpacağız.

43 x 100 = 4300
4300 x 100 = 430000 cm²

Örneğin 6200000 milimetrekare kaç metrekaredir?

Milimetrekareden metrekareye gitmek için 3 basamak sola gideriz.

Yani sayımızı 100’e üç kere böleceğiz.

6200000 : 100 = 62000
62000 : 100 = 620
620 : 100 = 6,2 m²

Arazi Ölçü Birimleri

• Öncelikle hektar (ha) – dekar (daa) – ar (a) sıralamasını bilmemiz gerekir.
• Bu sıralamada soldan sağa doğru giderken sayıyı her basamakta 10 ile çarparız.
• Sağdan sola doğru giderken sayıyı her basamakta 10’a böleriz.

1 dekar = 10 ar , 1 hektar = 10 dekar , 1 hektar = 100 ar

Hacim Ölçü Birimleri

• Alan ölçü birimleri m³ – dm³ – cm³ – mm³ şeklinde sıralanır.
• Bu sıralamada soldan sağa doğru giderken sayıyı her basamakta 1000 ile çarparız.
• Sağdan sola doğru giderken sayıyı her basamakta 1000’e böleriz.

Örneğin 7 metreküp kaç desimetreküptür?

Metreküpten desimetreküpe gitmek için 1 basamak sağa ineriz.

Yani sayıyı 1000 ile bir kere çarpacağız.

7 x 1000 = 7000 dm³

Örneğin

900000 santimetreküp kaç metreküptür?

Santimetreküpten metreküpe gitmek için 2 basamak sola gideriz.

Yani sayıyı 1000’e iki kere böleceğiz.

900000 : 1000 = 900
900 : 1000 = 0,9 m³

Sıvı Ölçme Birimleri

• Alan ölçü birimleri L – dL – cL – mL şeklinde sıralanır.
• Bu sıralamada soldan sağa doğru giderken sayıyı her basamakta 10 ile çarparız.
• Sağdan sola doğru giderken sayıyı her basamakta 10’a böleriz.

Örneğin 12 litre kaç desilitredir?

Litreden desilitreye gitmek için 1 basamak sağa ineriz.

Yani sayıyı 10 ile bir kere çarpacağız.

12 x 10 = 120 dL

Örneğin 500 santilitre kaç litredir?

Santilitreden litreye gitmek için 2 basamak sola gideriz.

Yani sayıyı 10’a iki kere böleceğiz.

500:10=50

50:10=5

Sıvı ölçü birimlerinde 1 L = 1 dm³ ‘e eşittir.

Temel Geometrik Kavramlar

Nokta: Geometrinin en temel kavramı olan noktayı kalem ucunun kağıtta bıraktığı iz olarak tanımlarız.

✅ Noktanın eni ,boyu ve yüksekliği yoktur. Tanımsız bir kavramdır.

✅ Nokta boyutsuzdur.

✅ Nokta büyük harf ile gösterilir.  · A   ( A noktası )

Noktanın noktaya göre konumunu tarif ederken ikinci söylenen noktadan başlanır.

 Örneğin ”E” noktasının ”D” noktasına göre konumu sorulduğunda  ikinci söylenen nokta olan ”D” noktasından başlayıp ”E” noktasına doğru yatay ve dikey gideriz.

Doğru: Her iki ucundan sonsuza kadar uzayan düz çizgiye doğru denir.

✅ Doğrunun başlangıç ve bitiş noktası yoktur. Bundan dolayı her iki ucuna ok konulur.

✅ Tek boyutludur.

✅ Doğrunun genişliği yoktur sadece uzunluğu vardır ama ölçülemez.

✅ Bir noktadan sonsuz doğru geçer.

✅ İki noktadan tek bir doğru geçer.

Doğru parçası: Her iki ucundan sınırlı düz çizgiye doğru parçası denir.

Doğru Parçasının Özellikleri

✅ Doğru parçasının başlangıcı ve sonu vardır.

✅ Genişliği yoktur ,uzunluğu vardır .Ölçülebilir.

✅ Tek boyutludur.

Işın: Bir ucu sınırlı diğer ucu sonsuza giden düz çizgiye ışın denir.

Işının Özellikleri

✅ Işının başlangıcı var ama sonu yoktur..

✅ Genişliği yoktur ,uzunluğu vardır .Ölçülemez.

✅ Tek boyutludur.

İki Doğrunun Birbirlerine Göre Durumları

• İki doğru birbirini tek bir noktada kesiyor ise bu doğrulara kesişen doğrular denir.
• Aynı düzlemde birbirini 90 derecelik açıyla kesen doğrulara dik doğrular denir. Dik doğrular  ” ⊥ ”  sembolü ile gösterilir. Dik doğrular aynı zamanda kesişen doğrulardır.
• Aynı düzlemde olup hiçbir noktada kesişmeyen doğrulara paralel doğrular denir. Paralel doğrular ”//” sembolü ile gösterilir.
• Aynı düzlemde olup tüm noktaları ortak olan doğrulara çakışık doğrular denir.
• Paralel doğruların arasındaki mesafeyi sıfıra indirdiğimizde çakışık doğrular olur. Çakışık doğrular birbirine paralel değildir.

Açı ve Açı Çeşitleri

Başlangıç noktaları aynı olan iki ışının birleşmesi ile arada kalan açıklığa açı denir.

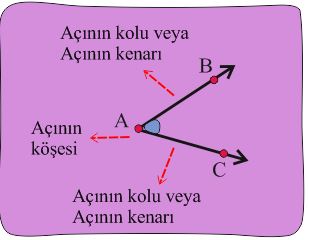
Açını ölçüsünü ”m” veya ”s” harfi kullanarak gösteririz. 

✅ m(A) veya s(A) 

➡️ ”A” açısının ölçüsü demektir.

Ölçüsü 0° ile 90° arasında olan açıya dar açı denir.

Ölçüsü 90° olan açıya dik açı denir.

lçüsü 90° ile 180° arasında olan açıya geniş açı denir.

Ölçüsü 180° olan açıya doğru açı denir.

Ölçüsü 360° olan açıya tam açı denir.

Olasılık ve İstatistik

Olasılık ve istatistik, matematiğin önemli bir dalıdır ve hayatımızın birçok alanında kullanılır. Örneğin, finansal piyasaların analizi, epidemiyolojik çalışmalar, oyun teorisi, yargı sistemleri, hava durumu tahminleri ve hatta spor analizleri gibi birçok alanda olasılık ve istatistik kullanılır. Bu terimler, belirli bir olayın gerçekleşme olasılığını hesaplamak ve belirli sonuçların analiz edilmesi için kullanılır. Veri analizi, hipotez testi, doğrusal regresyon ve varyans analizi gibi teknikler, istatistiksel analizin bir parçasıdır ve potansiyel sonuçları tahmin etmek için kullanılır.

Olasılık

Olasılık, matematikte bir olayın gerçekleşme olasılığının sayısal bir ifadesidir. Olasılık, 0 ile 1 arasında bir sayıdır ve genellikle P(A) şeklinde ifade edilir. Burada P(A), olay A’nın gerçekleşme olasılığını gösterir. Örneğin, bir zar atılması durumunda, her bir sayının gelme olasılığı 1/6’dır ve 0 ile 1 arasında bir değerle ifade edilebilir. Ayrıca, farklı olayların bir arada olasılığını hesaplamak için çeşitli olasılık kuralları da vardır.

✅ Bir olayın sonucunun ne olacağını görmek için yapılan işleme deney denir.

➡️ Bir zarın havaya atılması deneydir. Bir torbanın içinden rastgele bir top çekilmesi

✅ Bir deneyde elde edilebilecek sonuçların her birine çıktı denir.

➡️ Bir zarın havaya atılması deneyinde gelebilecek çıktılar 1,2,3,4,5 ve 6’dır. Bir madeni paranın havaya atılması deneyinde gelebilecek çıktılar yazı, tura ‘dır.

✅ Yapılan bir deney sonucunda karşılaşabileceğimiz her türlü durumlara olası durum denir.

➡️ Bir zarın havaya atılması deneyinde 6 olası durum vardır.

✅ Yapılan deney sonucunda meydana gelebilecek tüm çıktılara örnek uzay denir.

➡️ Bir zarın havaya atılması deneyinde örnek uzay 1,2,3,4,5,6’dır.

✅ Bir deneyin çıktıları arasından belirli bir şartı sağlayanlara olay denir.

➡️ Bir zarın havaya atılması deneyinde zarın 2’den küçük gelmesi olaydır.

✅ Bir deneye ait olası durum sayıları birbirlerine eşit olan olaylara eşit olasılıklı olaylar denir.

➡️ Bir zar havaya atıldığında zarın üst yüzüne gelen sayının tek olması ile ,3’den büyük olması eşit olasılıklı olaydır.

✅ Bir deneye ait iki farklı olayın olası durum sayıları biri diğerinden fazla olan olaya daha fazla olasılıklı olaylar denir. 

➡️ Aynı büyüklükteki 8 sütlü şeker ve 6 portakallı şeker bir torbaya atılıyor. Rastgele çekilen şekerin sütlü olması olayı portakallı olması olayından fazla olduğu için bu olaya daha fazla olasılıklı olay denir.

✅ Bir deneye ait iki farklı olayın olası durum sayılarının biri diğerinden az olan olaya daha az olasılıklı olaylar denir.

✅ Olasılık bir olayın gerçekleşmesinin veya gerçekleşmemesinin değeri veya ölçüsüdür. Bu ölçü gerçek bir sayıya eşittir. Bu sayı değeri en az 0 en fazla 1 olmak üzere 0 ile 1 arasındadır.

✅ Bir olay kesinlikle gerçekleşmiyor ise bu olaya imkansız olay denir. İmkânsız olayın olasılık değeri 0’dır.

✅ Bir olay kesinlikle gerçekleşiyor ise bu olaya kesin olay denir. Kesin olayın olasılık değeri 1’dir.

İstatistik

İstatistik, verilerin analizi için bir dizi matematiksel yöntemi içerir. İstatistik, verilerin değişkenliklerini ve eğilimlerini inceleyerek, belirli bir sonucun olasılığını hesaplayabilir. Örneğin, bir örneklemin medyanı veya ortalama değeri gibi istatistiksel ölçümler, belirli bir popülasyonun eğilimlerine dair bilgi sağlayabilir. İstatistiksel analiz ayrıca standart sapma, varyans ve korelasyon gibi ölçümleri değerlendirerek, verilerdeki ilişkileri ve değişkenlikleri tanımlayabilir.

Ayrıca, istatistiksel analiz siyah kutu testleri, regresyon analizi ve ANOVA gibi daha gelişmiş metotlar da içerir. Bu yöntemler daha karmaşık veri setleri için daha uygun olabilir ve genellikle bilimsel araştırmalarda kullanılır.

• Ortalama: Bir veri setinin tamamının toplamının veri sayısına bölünmesi ile elde edilir. Belli bir veri noktasının genel veri kümesinde ne kadar ortalama olduğunu belirlemek için kullanılır.
• Standart Sapma: Bir veri kümesinin ortalama değerinden ne kadar sapma gösterdiğini ölçmek için kullanılır. Daha yüksek bir standart sapma, verilerin daha değişken olduğunu gösterir.
• Medyan: Bir veri kümesinin ortasındaki değeri temsil eder. Verilerin ortasına yerleştirildiği için birçok analiz için ortalamadan daha güvenilir bir ölçümdür.
• Varyans: aritmetik ortalamadan standart sapma olarak da bilinen farkların karesinin ortalamasıdır. Basitçe söylemek gerekirse, varyans, bir veri gurubu içindeki veri noktalarının ne kadar yayılmış olduğunun istatistiksel bir ölçüsüdür.

Cebir

Cebir, matematiğin temel dallarından biridir ve geniş bir alana sahiptir. Bu dalın çözmeye çalıştığı problemlerin başında denklemler gelmektedir. Cebirde, polinomların faktörize edilmesi ve matrislerin çözümü de sıklıkla ele alınan konulardandır. Ayrıca, cebirsel ifadeler ve onların çeşitli işlemleri, modern matematikte yaygın olarak kullanılan tekniklerdir. Cebir, bütün bu alanları inceleyerek matematiğin birçok diğer dalıyla ilişkilidir.

Cebirsel İfadeler

➡️ İçerisinde en az bir bilinmeyen bulunan ifadelere cebirsel ifade denir. Değişkenler genellikle a,b,x,y,…. gibi küçük harfler kullanılarak gösterilir.

Fazıl’ın yaşı 18’dir. Fazıl’ın yaşının 3 katı ifadesi cebirsel ifade olmaz. Çünkü bilinmeyen bir ifade bulunmamaktadır.(Fazıl’ın yaşı biliniyor.)

Uğur’un yaşının 6 katı ifadesi cebirsel ifade  olur. Çünkü bilinmeyen ifade vardır. (Uğur’un yaşı bilinmiyor.)

➡️ Cebirsel ifadelerde bilinmeyen ifadeye değişken denir. Değişken harf yada sembol kullanılarak gösterilir.

➡️ Cebirsel ifadede ”+” veya ”-” işaretleri ile birbirinden ayrılan her bir ifadeye terim denir.

➡️ Cebirsel ifadede değişken içermeyen terime  sabit terim  denir.

➡️ Cebirsel ifadede değişkenlerle çarpım durumunda olan sayıya katsayı denir.

➡️ Cebirsel ifadede değişkenleri aynı olan terimlere benzer terim denir. Benzer terim olabilmesi için değişkenlerin üslerinin de  aynı olması lazım.

Denklemler

Denklemler matematikte önemli bir yere sahiptir ve birçok alanda kullanılır. x’in ne olduğunu bulma süreci, denklemleri çözmek olarak adlandırılır ve matematik deneyimine sahip olmanın temel becerilerinden biridir. Denklemler genellikle = işareti ile ayırt edilir ve cebirsel ifadelerin birinci dereceden olanları lineer denklemler, ikinci dereceden olanları kuadratik denklemler olarak adlandırılır. Denklemler, matematikte birçok problemi çözmek için kullanılan önemli bir araçtır.

Özdeşlik

İçindeki değişkenlere verilen bütün gerçek sayılar için doğru olan denklemlere özdeşlik denir.

Örneğin 3.(x − 2) = 3x − 6 eşitliğinde x yerine farklı değerler vererek eşitliğin sağlanıp sağlanmadığını kontrol edelim.

x yerine her iki eşitlikte 1 yazalım

3.(x − 2) = 3x − 6
3.(1 − 2) = 3.(1) − 6
−3 = −3

x yerine her iki eşitlikte 2 yazalım

3.(x − 2) = 3x − 6
3.(2 − 2) = 3.(2) − 6
0 = 0

Görüldüğü gibi soldaki eşitlik x yerine yazdığımız iki değer içinde eşitlik sağlandı.

Bu yüzden: 3.(x − 2) = 3x − 6 bir özdeşliktir.

Lineer Denklemler

Lineer denklemler, x’in birinci dereceden bir cebirsel ifadesini içeren denklemlerdir. Genellikle Ax + B = 0 şeklinde yazılırlar.

Kuadratik Denklemler

Kuadratik denklemler, x’in ikinci dereceden bir cebirsel ifadesini içeren denklemlerdir. Genellikle Ax²+Bx+C=0 şeklinde yazılırlar.

Kuadratik formül, herhangi bir parabolün köklerini veren bir formüldür.

Lineer Denklemler

Lineer denklemler, iki bilinmeyenli cebirsel denklemlerden daha az bilinmeyeni olan ve x’in birinci dereceden bir cebirsel ifadesini içeren denklemlerdir. Genellikle kabul edilen standart formu Ax+B=0 şeklindedir. Burada, A ve B, sırasıyla x’nin katsayısı ve sabit sayıdır. Lineer denklemler, matematikte sıklıkla kullanılan ve birçok gerçek dünya probleminin çözümü için gerekli bir özelliktir.

Bir denklemin lineer denklem olması için:
➡️ değişkenler yalnızca 1. dereceden olmalı,
➡️ bağımlı ve bağımsız değişkenler çarpım durumunda olmamalı,
➡️ denklem, değişkenlerin trigonometrik veya logaritmik fonksiyonlarını içermemelidir.

Resim Gerd Altmann tarafından Pixabay‘a yüklendi. Matematik Terimlerini sizler için derledik. Fikrinizi yorumda belirtebilirsiniz.

Geometrik Cisimler

Uzayda birbirine eş ve paralel iki çokgenin karşılıklı köşelerinin doğrularla birleştirilmesiyle elde edilen geometrik cisme prizma denir.

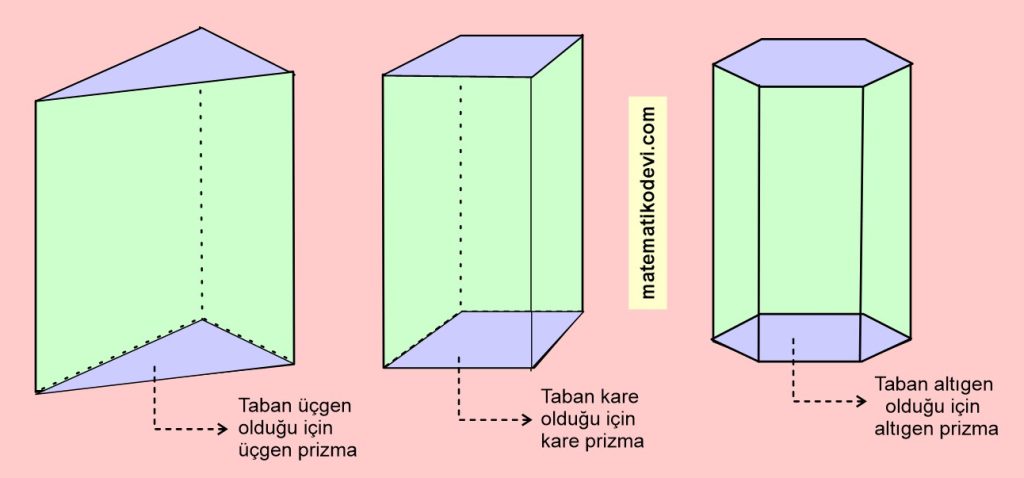
Prizmanın temel elemanları; taban, yanal yüz ( yan yüzey) , ayrıt, köşe ve yüksekliktir.

Üçgen prizma 

Yüz Sayısı👉 5
Taban Sayısı👉 2
Köşe Sayısı👉 6
Toplam Ayrıt Sayısı👉 9

Dikdörtgen prizma 

Yüz Sayısı 👉 6
Taban Sayısı 👉 2
Köşe Sayısı 👉 8
Toplam Ayrıt Sayısı 👉 12

Beşgen prizma 

Yüz sayısı 👉 7
Taban sayısı 👉 2
Köse sayısı 👉 10
Toplam ayrıt sayısı 👉15

Silindir

• Silindirin temel elemanları; tabanları, yanal yüzeyi, ana doğrular, eksen, yarıçap ve yüksekliktir.
• Silindirde alt ve üst kısmında yer alan eş dairelere taban denir.
• Tabanları oluşturan dairelerin yarıçapları silindirin yarıçapıdır ve “r” ile gösterilir.
• Tabanlardaki dairelerin merkezlerini birleştiren doğru parçasına eksen denir.
• Üst tabanın bir noktasından alt tabandaki bir noktaya indirilen dikmeye yükseklik denir ve bu yükseklik “h” ile gösterilir.
• Dik dairesel silindirin ekseni tabana dik olduğu için eksen aynı zamanda yüksekliktir. (eksen=yükseklik)
• Tabanların karşılıklı iki noktasını bileştiren ve eksene paralel olan doğru parçalarına ana doğru denir.
• Silindirin tabanı dışındaki görünen yüze yanal yüzey (yan yüzey) denir.

Piramait

Tabanını herhangi bir çokgensel bölgenin oluşturduğu, yanal ayrıtları aynı tepede bir noktada birleşen kapalı cisimlere piramit denir.

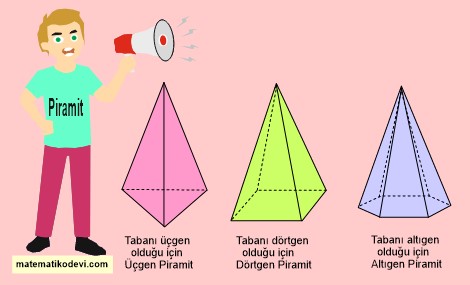
Piramidin temel elemanları;

Yanal ayrıtların kesiştikleri nokta tepe noktasıdır.

Ayrıtların kesiştikleri noktalar piramidin köşeleridir. Tepe noktası aynı zamanda köşedir.

Tabanı oluşturan çokgenin kenarlarına taban ayrıtı denir.

Tabanın köşelerini tepe noktasına birleştiren doğru parçalarına yanal ayrıt denir.

Tepe noktasının tabana olan uzaklığı piramidin yüksekliğidir.

Tepe noktasının tabana olan uzaklığı piramidin yüksekliğidir.