Kareköklü Bir Sayıyı a kök b Şeklinde Yazma Konu Anlatımı

Bilgi: Kareköklü bir sayıyı a√b şeklinde yazmak için ;

✅ Karekök içindeki sayı çarpanlarından en az biri yazılabilecek en büyük tam kare sayı olacak şekilde iki sayının çarpımı şeklinde yazılır.

✅ Tam kare olan çarpanın karekökü karekök dışına katsayı olarak yazılır.

✅ Tam kare olmayan çarpan karekök içinde kalır.

Örnek: Aşağıdaki kareköklü ifadeleri akatex is not defined şeklinde yazalım.

➡ katex is not defined = ?

✅ 12’yi birisi tam kare olmak şartıyla iki sayının çarpımı şeklinde karekökün içine yazarız.

katex is not defined

🤓 12’yi tam kare olan 4’ün çarpımı şeklinde yazdım.

✅ Tam kare olan çarpanın karekökü karekök dışına katsayı olarak yazılır.

2katex is not defined

🤓 Tam kare olan 4’ün karekökünü (katex is not defined = 2) karekök dışına yazdım.

✅ Tam kare olmayan çarpan karekök içinde kalır.

2katex is not defined

🤓 Tam kare olmayan çarpanı (3’ü) karekök içinde bıraktım.

➡ katex is not defined = ?

✅ 75’i birisi tam kare olmak şartıyla iki sayının çarpımı şeklinde karekökün içine yazarız.

katex is not defined

🤓 25’i tam kare olan 25’in çarpımı şeklinde yazdım.

✅ Tam kare olan çarpanın karekökü karekök dışına katsayı olarak yazılır.

5katex is not defined

🤓 Tam kare olan 25’in karekökünü (katex is not defined = 5) karekök dışına yazdım.

✅ Tam kare olmayan çarpan karekök içinde kalır.

5katex is not defined

🤓 Tam kare olmayan çarpanı (3’ü) karekök içinde bıraktım.

➡ katex is not defined = ?

✅ 98’i birisi tam kare olmak şartıyla iki sayının çarpımı şeklinde kökün içine yazarız.

katex is not defined

🤓 98’i tam kare olan 49’un çarpımı şeklinde yazdım.

✅ Tam kare olan çarpanın karekökü karekök dışına katsayı olarak yazılır.

7katex is not defined

🤓 Tam kare olan 49’un karekökünü (katex is not defined = 7) karekök dışına yazdım.

✅ Tam kare olmayan çarpan karekök içinde kalır.

7katex is not defined

🤓 Tam kare olmayan çarpanı (2’yi) karekök içinde bıraktım.

Bilgi: Tam kare olmayan sayıyı asal çarpanlarına ayırarak a√b şeklinde yazmak için ;

✅ Kök içindeki sayıyı asal çarpanlarına ayırırız.

✅ Sonra sayıyı kök içinde asal çarpanları şeklinde yazarız..

✅ Sonra kök içindeki her ikili sayıyı tekli sayı olarak kök dışına çıkarırız. Tekli olan sayılar kök içinde kalır.

✅ Örneğin √3×3×5 = 3√5 (kök içindeki iki tane 3 kök dışına 1 tane 3 olarak çıktı.)

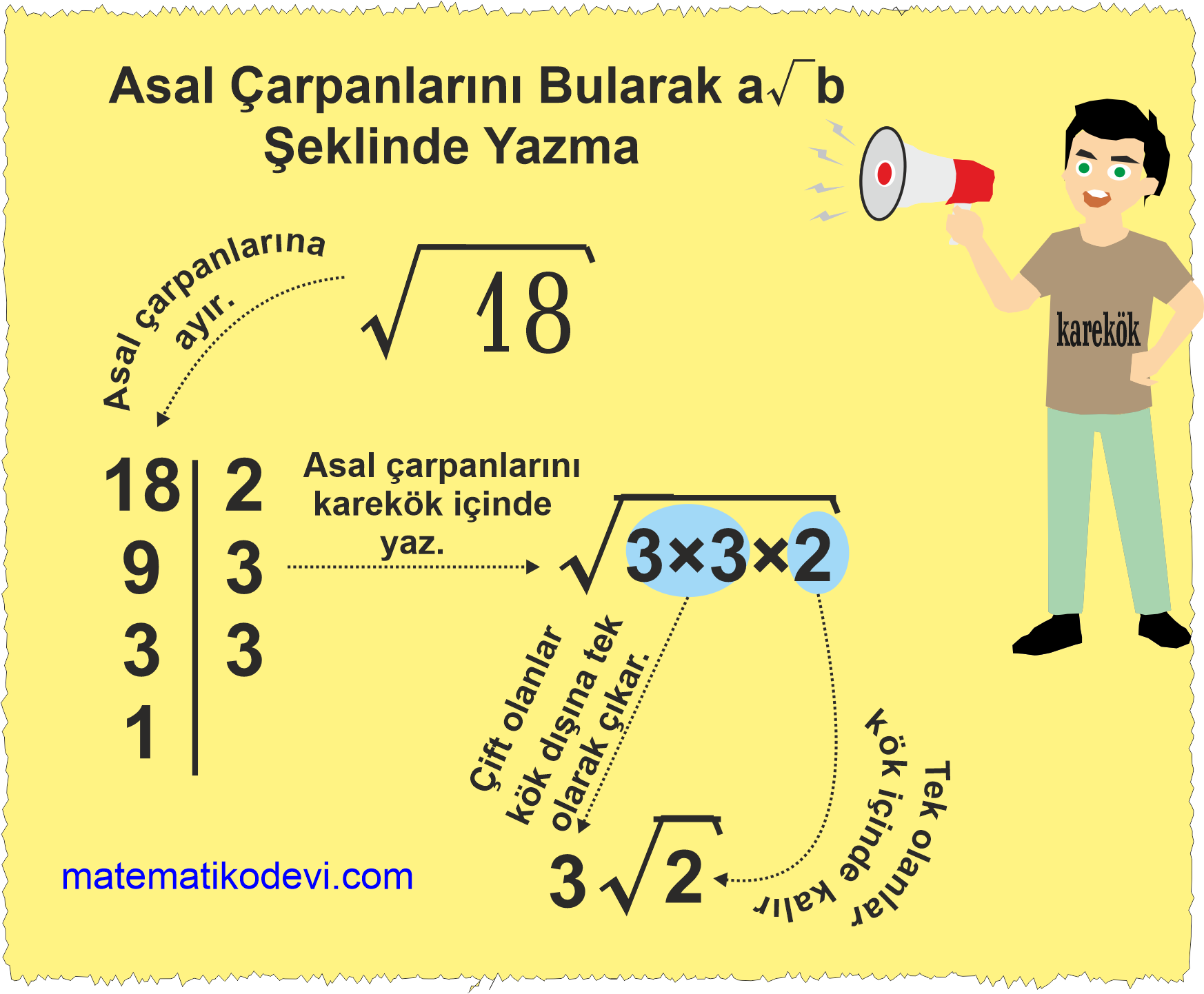
Örnek: Aşağıdaki kareköklü ifadeleri asal çarpanlarını bularak akatex is not defined şeklinde yazalım.

➡ katex is not defined

✅ 48’i asal çarpanlarına ayıralım.

✅ Asal çarpanlarını karekök içinde yaz.

✅ Kök içinde olan her ikili sayı kök dışına tekli olarak çıkar , kök içinde tekli olan sayılar kök içine kalır.

✅ Kök dışındaki sayıları çarparız.

➡ katex is not defined

✅ 360’ı asal çarpanlarına ayıralım.

✅ Asal çarpanlarını karekök içinde yaz.

✅ Kök içinde olan her ikili sayı kök dışına tekli olarak çıkar , kök içinde tekli olan sayılar kök içine kalır.

✅ Kök dışındaki ve kök içindeki sayıları çarparız.

Örnek: Aşağıdaki kareköklü ifadeleri akatex is not defined şeklinde yazalım.

➡ katex is not defined = ?

✅ Üssü olabilecek en büyük çift sayı şeklinde parçalayım

katex is not defined

✅ Çift olan üssün yarısı kök dışına , tek olan üssü kök içine yazarız.

5³katex is not defined

125 katex is not defined

➡ katex is not defined = ?

✅ Üssü olabilecek en büyük çift sayı şeklinde parçalayım

katex is not defined

✅ Çift olan üssün yarısı kök dışına , tek olan üssü kök içine yazarız.

6⁴katex is not defined

6⁴ katex is not defined

➡ katex is not defined = ?

✅ Üssü olabilecek en büyük çift sayı şeklinde parçalayım

katex is not defined

✅ Çift olan üssün yarısı kök dışına , tek olan üssü kök içine yazarız.

7²katex is not defined

49 katex is not defined

➡ katex is not defined = ?

✅ Üs çift olursa kök içindeki sayıların tamamı kök dışına çıkar kök içinde sayı kalmaz.

katex is not defined = 3⁴

Bilgi: a√b şeklindeki ifadelerde a’yı (katsayıyı) kök içine almak için a’yı iki defa çarparız.

✅ a√b = √a×a×b

Örnek: Aşağıdaki akatex is not defined şeklindeki ifadelerin katsayılarını kök içine alalım.

➡ 2katex is not defined = ?

✅ Katsayı olan 2’yi kök içine almak için iki defa çarpmamız lazım.

katex is not defined

katex is not defined

➡ 4katex is not defined = ?

✅ Katsayı olan 4’ü kök içine almak için iki defa çarpmamız lazım.

katex is not defined

katex is not defined

➡ 3katex is not defined = ?

✅ Katsayı olan 3’ü kök içine almak için iki defa çarpmamız lazım.

katex is not defined

katex is not defined

[alert color=”danger”]Not: Kareköklü sayılarda sıralama yaparken;

✅ a√b şeklindeki ifadelerde katsayıyı kök içine alırız.

✅ Bütün sayılar kök içindeyse kök yokmuş gibi düşünüp sayıları sıralarız. [/alert]

Örnek: Aşağıdaki sayıları küçükten büyüğe doğru sıralayınız.

➡ 6katex is not defined , katex is not defined , 3katex is not defined

✅ a√b şeklindeki ifadelerde katsayıyı kök içine alırız.

6katex is not defined = katex is not defined = katex is not defined

katex is not defined Karekök dışında sayı yok

3katex is not defined = katex is not defined = katex is not defined

✅ Bütün sayılar kök içindeyse kök yokmuş gibi düşünüp sayıları sıralarız. [/alert]

6katex is not defined = katex is not defined

katex is not defined

3katex is not defined = katex is not defined

63<70<72 olduğu için 3katex is not defined < katex is not defined < 6katex is not defined

➡ 5katex is not defined , 4katex is not defined , 9katex is not defined

✅ a√b şeklindeki ifadelerde katsayıyı kök içine alırız.

5katex is not defined = katex is not defined = katex is not defined

4katex is not defined = katex is not defined = katex is not defined

9katex is not defined = katex is not defined = katex is not defined

✅ Bütün sayılar kök içindeyse kök yokmuş gibi düşünüp sayıları sıralarız. [/alert]

5katex is not defined = katex is not defined

4katex is not defined = katex is not defined

9katex is not defined = katex is not defined

112<150<162 olduğu için 4katex is not defined < 5katex is not defined < 9katex is not defined

➡ 2katex is not defined , 7 , 3katex is not defined

✅ a√b şeklindeki ifadelerde katsayıyı kök içine alırız.

2katex is not defined = katex is not defined = katex is not defined

7 = katex is not defined = katex is not defined

3katex is not defined = katex is not defined = katex is not defined

✅ Bütün sayılar kök içindeyse kök yokmuş gibi düşünüp sayıları sıralarız. [/alert]

2katex is not defined = katex is not defined

7 = katex is not defined

3katex is not defined = katex is not defined

44<45<49 olduğu için 3katex is not defined < 3katex is not defined < 7