Tam Kare Olmayan Sayıların Karekökleri Konu Anlatımı
Kazanım: Tam kare olmayan kareköklü bir sayının hangi iki doğal sayı arasında olduğunu belirler.
Tam Kare Olmayan Sayıların Karekökleri Konu Anlatımı aşağıda detaylı şekilde yapılmıştır. Konu tamamladıktan sonra sizin için hazırladığımız yeni nesil soruları çözmeyi ve video çözümü izlemeyi unutmayınız.
Bu konuda neler öğreneceğiz :
Tam Kare Olmayan Sayıları Bulma
Bir önceki konumuzda 1,4,9,16,25,36,49… gibi sayılara tam kare sayılar denildiğini öğrenmiştik. Bu sayılar dışında kalan bütün sayılara tam kare olmayan sayılar denir.Yani iki tam kare sayı arasında olan sayıların hepsine tam kare olmayan sayılar denir.Aşağıdaki görselde tam kare ve tam kare olmayan sayılara örnek verilmiştir.

Örnek: Aşağıda verilen kareköklü sayılardan tam kare olmayan sayıları bulalım.
✅ \sqrt {20} =?
➡ \sqrt {20} sayısı 16 tam kare sayısı ile 25 tam kare sayısı arasındadır.
🤔 \sqrt {20} sayısı tam kare değildir.
✅ \sqrt {32} =?
➡ \sqrt {32} sayısı 25 tam kare sayısı ile 36 tam kare sayısı arasındadır.
🤔 \sqrt {32} sayısı tam kare değildir.
✅ \sqrt {68} =?
➡ \sqrt {68} sayısı 64 tam kare sayısı ile 81 tam kare sayısı arasındadır.
🤔 \sqrt {68} sayısı tam kare değildir.
Tam Kare Olmayan Sayıların Hangi İki Tam Sayı Arasında Olduğunu Bulma
Bilgi: Tam kare olmayan sayıların kareköklerinin hangi tam sayılar arasında olduğunu bulmak için ;
✅ Verilen sayıdan küçük ilk tam kare sayıyı buluruz.
✅ Verilen sayıdan büyük ilk tam kare sayıyı buluruz.
✅ Verilen sayı bu iki tam kare sayı arasındadır.
Tam kare sayıların karekökleri doğal sayıdır.Tam kare olmayan sayıların karekökleri ise iki doğal sayının arasındadır.
Örneğin \sqrt {4} =2 doğal sayısına eşit ve \sqrt {9} =3 doğal sayısına eşittir.
\sqrt {4} ile \sqrt {9} arasında olan \sqrt {5} , \sqrt {6} , \sqrt {7} , \sqrt {8} sayıları 2 ile 3 arasındadır.Bu şekilde tam kare olmayan sayıların hangi iki tam sayı arasında olduğunu bulabiliriz.
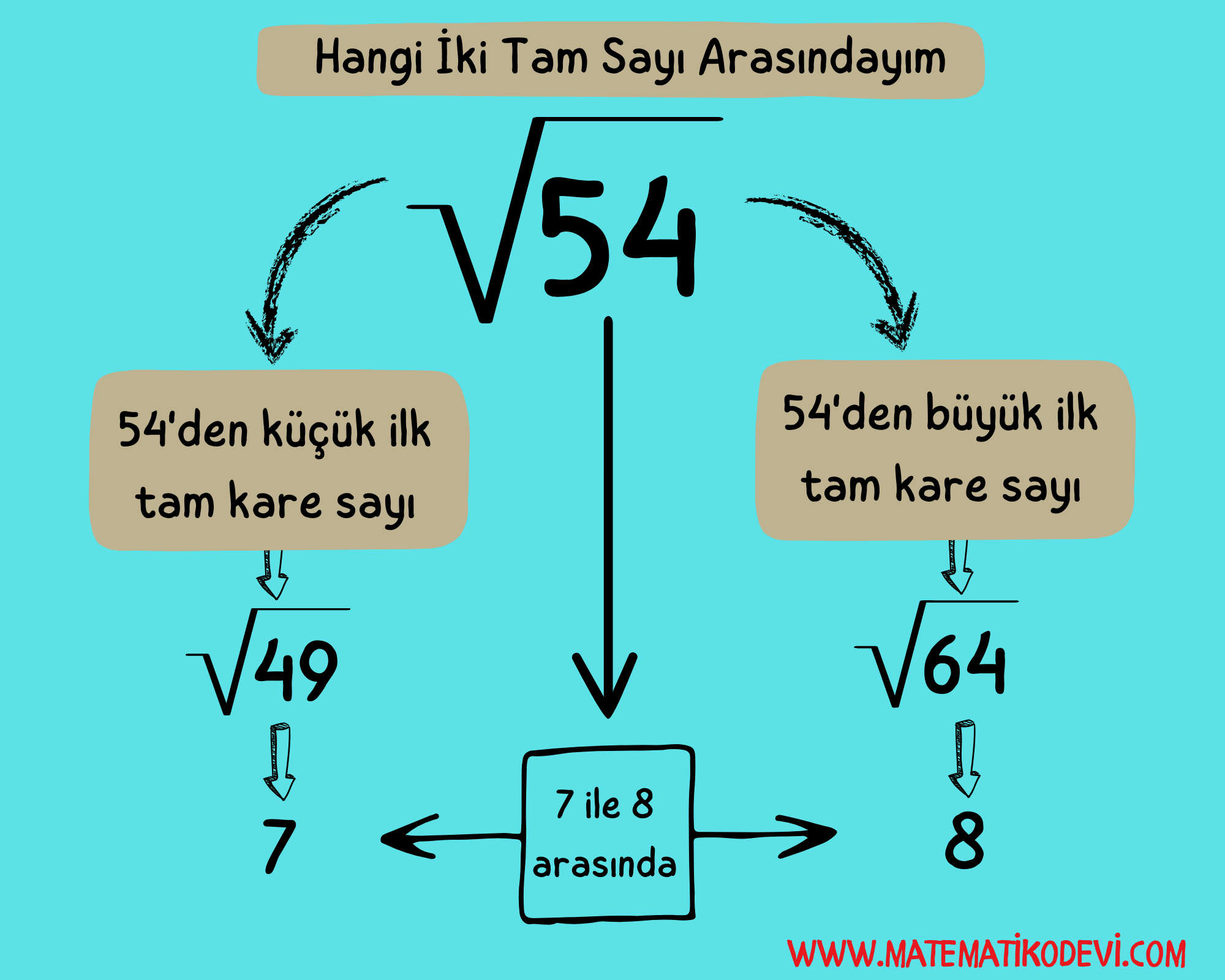
Örnek: Aşağıda verilen kareköklü sayıların hangi iki tam sayı arasında olduğunu bulalım.
➡ \sqrt {27} = ?
✅ Verilen sayıdan küçük ilk tam kare sayıyı buluruz.
\sqrt {27} ‘den küçük ilk tam kare sayı \sqrt {25} = 5
✅ Verilen sayıdan büyük ilk tam kare sayıyı buluruz.
\sqrt {27} ‘den büyük ilk tam kare sayı \sqrt {36} = 6
✅ Verilen sayı bu iki tam kare sayı arasındadır.
\sqrt {27} sayısı 5 ile 6 arasındadır.
➡ \sqrt {48} = ?
✅ Verilen sayıdan küçük ilk tam kare sayıyı buluruz.
\sqrt {48} ‘den küçük ilk tam kare sayı \sqrt {36} = 6
✅ Verilen sayıdan büyük ilk tam kare sayıyı buluruz.
\sqrt {48} ‘den büyük ilk tam kare sayı \sqrt {49} = 7
✅ Verilen sayı bu iki tam kare sayı arasındadır.
\sqrt {48} sayısı 6 ile 7 arasındadır.
➡ \sqrt {91} = ?
✅ Verilen sayıdan küçük ilk tam kare sayıyı buluruz.
\sqrt {91} ‘den küçük ilk tam kare sayı \sqrt {81} = 9
✅ Verilen sayıdan büyük ilk tam kare sayıyı buluruz.
\sqrt {91} ‘den büyük ilk tam kare sayı \sqrt {100} = 10
✅ Verilen sayı bu iki tam kare sayı arasındadır.
\sqrt {91} sayısı 9 ile 10 arasındadır.
Not: Kök içindeki tam kare olmayan sayı komşu tam kare sayılardan hangisine daha yakın ise o tam kare sayının kareköküne daha yakındır.
Yukarıdaki notu bir örnekle açıklayalım. ⤵️
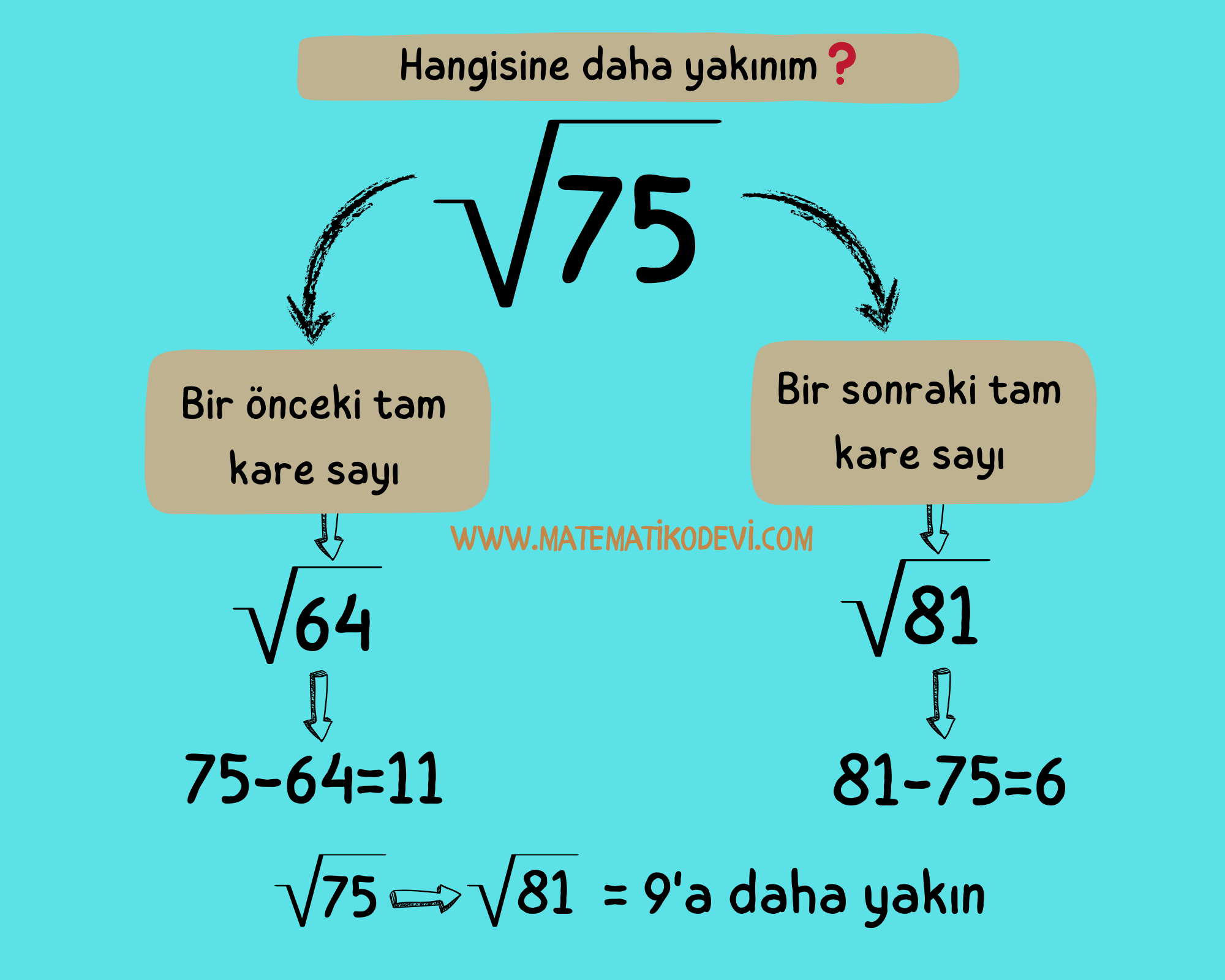
Örnek: \sqrt {43} sayısı hangi tam sayıya daha yakın olduğunu bulalım.
➡ \sqrt {43} ‘den önceki tam kare sayı \sqrt {36}
➡ \sqrt {43} ‘den sonraki tam kare sayı \sqrt {49}
➡ Şimdi hangisine yakın olduğunu bulalım
➡ 43-36=7
➡ 49-43=6
➡ \sqrt {43} sayısı \sqrt {49} =7 sayısına daha yakın
Tam Kare Olmayan Sayıların Yaklaşık Değerini Bulma
Bilgi: Tam kare olmayan bir sayının karekökünün yaklaşık değerini bulurken;
✅ Verilen sayıdan bir önceki tam kare sayının karekökü tam kısım
✅ Verilen sayının kök içindeki sayısı ile bir önceki tam kare sayının farkı pay
✅ Verilen sayıdan bir sonraki tam kare sayı ile bir önceki tam kare sayının farkı payda
olarak yazdığımızda verilen sayının karekökünün yaklaşık değerini buluruz.

Örnek: Aşağıda verilen tam kare olmayan sayıların karekökünün yaklaşık değerini bulalım.
➡ \sqrt {38} = ?
\sqrt {36} < \sqrt {38} < \sqrt {49}
✅ Verilen sayıdan bir önceki tam kare sayının karekökü tam kısım
\sqrt {36} =6 (tam kısım)
✅ Verilen sayının kök içindeki sayısı ile bir önceki tam kare sayının farkı pay
38-36=2 (pay)
✅ Verilen sayıdan bir sonraki tam kare sayı ile bir önceki tam kare sayının farkı payda
49-36=13 (payda)
\sqrt {38} sayısının yaklaşık değeri 6 \dfrac{2}{13} = 6,15
➡ \sqrt {76} = ?
\sqrt {64} < \sqrt {76} < \sqrt {81}
✅ Verilen sayıdan bir önceki tam kare sayının karekökü tam kısım
\sqrt {64} =8 (tam kısım)
✅ Verilen sayının kök içindeki sayısı ile bir önceki tam kare sayının farkı pay
76-64=12 (pay)
✅ Verilen sayıdan bir sonraki tam kare sayı ile bir önceki tam kare sayının farkı payda
81-64=17 (payda)
\sqrt {76} sayısının yaklaşık değeri 8 \dfrac{12}{17} = 8,7
➡ \sqrt {105} = ?
\sqrt {100} < \sqrt {105} < \sqrt {121}
✅ Verilen sayıdan bir önceki tam kare sayının karekökü tam kısım
\sqrt {100} =10 (tam kısım)
✅ Verilen sayının kök içindeki sayısı ile bir önceki tam kare sayının farkı pay
105-100=5 (pay)
✅ Verilen sayıdan bir sonraki tam kare sayı ile bir önceki tam kare sayının farkı payda
121-100=21 (payda)
\sqrt {105} sayısının yaklaşık değeri 10 \dfrac{5}{21} = 10,23

Tam Kare Olmayan Sayıların Karekökleri Test ve Etkinlik
⚠️Test ve Etkinlikler açılmamış olursa sayfayı yenileyiniz.
Yeni Nesil Soru
🎥 Bir Soru Bir Video 🎥
Soru:

Yukarıda üst üste dizilmiş 5 blok verilmiştir. Bu blokların bazılarının yükseklikleri aşağıdaki tabloda verilmiştir.
| Blok | Yükseklik |
| A | 3 cm |
| B | 4 cm |
| C | ? cm |
| D | ? cm |
| E | 5 cm |
A bloğunun en altından başlayıp yukarı doğru \sqrt {90} cm çıkıldığında D bloğunun üzerinde bir yere , E bloğunun en üstünden başlayıp aşağı doğru \sqrt {130} cm inildiği zaman C bloğunun üzerinde bir yere ulaşılmıştır.
Buna göre C ve D bloklarının yükseklikleri tam sayı cinsinden en az kaç cm olabilir?
| A) | C= 3 cm | D= 6 cm |
| B) | C= 3 cm | D= 5 cm |
| C) | C= 2 cm | D= 7 cm |
| D) | C= 2 cm | D= 6 cm |
Çözüm:

