Eşit Şansa Sahip Olan Olaylar ve Basit Olayların Olasılıklarını Hesaplama Konu Anlatımı
Kazanım: Eşit şansa sahip olan olaylarda her bir çıktının olasılık değerinin eşit olduğunu ve bu değerin 1/n olduğunu açıklar.
Eşit Şansa Sahip Olan Olaylar ve Basit Olayların Olasılıklarını Hesaplama Konu Anlatımı aşağıda anlatılmıştır. Konuyu öğrendikten sonra yeni nesil sorumuzu çözmeyi unutmayın. 🤓
Bu konuda neler öğreneceğiz :
Eşit Şansa Olan Sahip Olaylar ve Basit Olayların Olasılıklarını Hesaplama
Bir torbanın içine farklı renklerde top atalım ve bu toplardan biri diğerlerinden büyük olsun. Bu torbanın içinden bir top çektiğimizde büyük olan top diğer toplara göre daha avantajlıdır. Yani bu torbadaki toplar eşit şansa sahip değildir. Bu yüzden olasılık sorularında paralar hilesiz, toplar eşit büyüklükte…. gibi çıktıların eşit şansta olması gerekir.
Bilgi: İki veya daha fazla çıktının olasılık değerlerinin eşit olduğu olaylara eşit şansa sahip olaylar denir.
✅ Eşit şansa sahip olaylardaki olasılık değeri 1/n olarak hesaplanır.
✅ ”n” olası durum sayısını ifade eder.
Örnek: Hilesiz bir zar havaya atılıyor.

Buna göre;
➡ Olası durum sayısı (n) = 6
➡ Üst yüze 1 gelme olasılığı \dfrac{1}{6}
➡ Üst yüze 2 gelme olasılığı \dfrac{1}{6}
➡ Üst yüze 3 gelme olasılığı \dfrac{1}{6}
➡ Üst yüze 4 gelme olasılığı \dfrac{1}{6}
➡ Üst yüze 5 gelme olasılığı \dfrac{1}{6}
➡ Üst yüze 6 gelme olasılığı \dfrac{1}{6}
Örnek: Eşit büyüklükteki topların olduğu torbadan bir top çekiliyor.
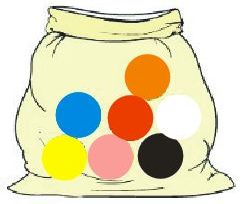
Buna göre;
➡ Olası durum sayısı (n) = 7
➡ Topun sarı olma olasılığı \dfrac{1}{7}
➡ Topun mavi olma olasılığı \dfrac{1}{7}
➡ Topun kırmızı olma olasılığı \dfrac{1}{7}
➡ Topun pembe olma olasılığı \dfrac{1}{7}
➡ Topun siyah olma olasılığı \dfrac{1}{7}
➡ Topun beyaz olma olasılığı \dfrac{1}{7}
➡ Topun turuncu olma olasılığı \dfrac{1}{7}
Örnek: Aşağıda verilen eşit bölmeli çark rastgele çevriliyor.

Buna göre ;
➡ Olası durum sayısı (n) = 8
➡ 1. A ‘nın gelme olasılığı \dfrac{1}{8}
➡ 2. A ‘nın gelme olasılığı \dfrac{1}{8}
➡ 3. A ‘nın gelme olasılığı \dfrac{1}{8}
➡ 4. A ‘nın gelme olasılığı \dfrac{1}{8}
➡ B ‘nin gelme olasılığı \dfrac{1}{8}
➡ 1. C ‘nin gelme olasılığı \dfrac{1}{8}
➡ 2. C ‘nin gelme olasılığı \dfrac{1}{8}
➡ 3. C ‘nin gelme olasılığı \dfrac{1}{8}
😎 Her bir çıktının olasılığı eş olasılıklı iken her harfin olasılığı eş olasılıklı olmayabilir. 😎
➡ A’nın gelme olasılığı \dfrac{4}{8}
➡ B ‘nin gelme olasılığı \dfrac{1}{8}
➡ C ‘nin gelme olasılığı \dfrac{3}{8}
Yeni Nesil Soru
🎥 Bir Soru Bir Video 🎥
Soru: Aşağıda 3 farklı renkte kartlar verilmiştir.

Aynı renge sahip olan kartların alanları birbirine eşittir.Bu kartlardan eşit şansa sahip ve olası durumu en fazla olan kartlar seçiliyor.Seçilen kartlara , kartlar bitene kadar sırayla 1,2,3,1,2,3 yazılıyor.
Buna göre üzerinde 1,2 ve 3 yazılı olan kartlar arasından bir kart seçildiğinde kartın üzerinde 2 yazma olasılığı kaçtır?
A) \dfrac{2}{6}\quad \quad B) \dfrac{1}{8}\quad \quad C) \dfrac{2}{5}\quad \quad D) \dfrac{3}{8}\quad \quad
Çözüm:

