EBOB EKOK Konu Anlatımı
Kazanım: İki doğal sayının en büyük ortak bölenini (EBOB) ve en küçük ortak katını (EKOK) hesaplar; ilgili problemleri çözer.
Bu konuda neler öğreneceğiz :
EBOB EKOK KONU ANLATIMI
EBOB ”en büyük ortak bölen” ifadesinin , EKOK ise ” en küçük ortak kat” ifadesinin baş harflerinin kısaltılması ile oluşmuş matematik terimidir. EBOB EKOK konu anlatımı aşağıda detaylı bir şekilde inceleyelim.
En Büyük Ortak Böleni Bulma
Bilgi: İki ya da daha fazla doğal sayının ortak bölenlerinin en büyüğüne bu sayıların en büyük ortak böleni denir. En Büyük Ortak Böleni kısaca “EBOB“ şeklinde ifade ederiz.
✅ x ve y tam sayılarının en büyük ortak bölenini EBOB(x,y) veya (x,y)ebob şeklinde gösterilir.
Örnek: 27 ve 36 sayılarının en büyük ortak bölenini bulalım.
➡️ Öncelikle 27 ve 36 sayılarının pozitif bölenlerini yazalım.
27’nin pozitif tam sayı bölenleri: 1, 3, 9, 27
36’nın pozitif tam sayı bölenleri: 1, 2, 3, 4, 6, 9, 12,18,36
➡️ 27 ve 36 ‘nın ortak bölenlerini yazalım.
27 ve 36’nın ortak bölenleri : 1,3,9
➡️ Bu ortak bölenlerin en büyüğüne EBOB denir.
27 ve 36’nın En Büyük Ortak Böleni 9’dur.
Bunu EBOB(27,36)=9 veya (27,36)EBOB =9 şeklinde ifade ederiz.
Örnek: 28 ve 42 sayılarının en büyük ortak bölenini bulalım.
➡️ Öncelikle 28 ve 42 sayılarının pozitif bölenlerini yazalım.
28’in pozitif tam sayı bölenleri: 1, 2, 4,7,14,28
42’nin pozitif tam sayı bölenleri: 1, 2, 3, 6, 7, 14, 21,42
➡️ 28 ve 42’nin ortak bölenlerini yazalım.
28 ve 42’nin ortak bölenleri : 1,2,14
➡️ Bu ortak bölenlerin en büyüğüne EBOB denir.
28 ve 42’nin En Büyük Ortak Böleni 14’dür.
Bunu EBOB(28,42)=14 veya (28,42)EBOB =14 şeklinde ifade ederiz.
✅ Verilen sayıların en büyük ortak bölenini (EBOB) asal çarpan algoritması yöntemi ile bulabiliriz. Bu yöntemin adım adım açıklaması aşağıdaki gibidir.
Örneğin 30 ve 45 sayısını en büyük ortak bölenini (EBOB) bulalım.
➡️ Bu yöntemde sayılar yan yana yazılarak bölen listesi yapılır ve sayılar bölünebilen en küçük asal sayıya bölünür. (sayılardan 1 tanesinin bölünmesi yeterli)

➡️Sayılardan hiç biri ilk böldüğümüz asal sayıya bölünmüyorsa bir sonraki asal sayıya geçilir.

➡️ Verilen sayıların ikisi de aynı anda bölünüyorsa sayıları bölen asal sayıya işaret koyulur.

➡️ İki sayı da 1 olana kadar işleme devam edilir.

➡️ İşaretli olan sayıların çarpımı En Büyük Ortak Böleni (EBOB) verir.

ÖRNEK: 36 ve 54 sayılarının EBOB’unu asal çarpanlar algoritması yöntemiyle bulalım.
ÇÖZÜM:

Not: Birbirinin katı olan iki doğal sayının EBOB’u her zaman küçük olan sayıya eşittir.
✅ Örneğin 20 ve 60 sayısının EBOB’u 20’dir.
Örnek: Aşağıda birbirinin katı olan sayılar verilmiştir.
Buna göre bu sayıların EBOB’unu kısa yoldan bulunuz.
✅ 15 ve 45 sayılarının EBOB’unu bulunuz.
➡️ 15 sayısı 45 sayısının katı olduğu için bu iki sayının EBOB’u küçük olan sayıya eşittir.
➡️ EBOB(15,45)=15
✅ 30 ve 60 sayılarının EBOB’unu bulunuz.
➡️ 30 sayısı 60 sayısının katı olduğu için bu iki sayının EBOB’u küçük olan sayıya eşittir.
➡️ EBOB(30,60)=30
Not: Asal çarpan algoritmasında harfli olarak verilen iki doğal sayının EBOB’unu bulurken harflerin değişip değişmemesine bakarız. İki harf aynı anda değişirse bölen sayı ortak bölendir.

Not: Verilen sayıların hiç ortak asal böleni yoksa EBOB’ları 1 kabul edilir. Çünkü 1 her doğal sayının ortak bölenidir. EBOB’u 1 olan bu sayılara aralarında asal sayılar denir.
Örnek: 48 ve 35 sayılarının EBOB’unu bulalım.
Çözüm:
➡️ 48’in bölenleri:1,2,3,4,6,8,12,16,24,48
➡️ 35’in bölenleri:1,5,7,35
➡️ 48 ve 35’in ortak böleni 1’dir.
➡️ EBOB(35,48)=1
➡️ EBOB(35,48)=1 olduğu için 35 ve 48 sayıları aralarında asal sayılardır.
Not: Asal çarpanlarına ayrılmış şekilde verilen ifadelerin EBOB’unu bulurken ortak olan tabanlardan üssü en küçük olanı seçeriz. Sonra bu sayıları çarptığımızda verilen sayıların EBOB’unu buluruz.

Örnek: Asal çarpanlara ayrılmış hali A = 23×32 ve B = 24×31×52 olan A ve B sayılarının en büyük ortak bölenini bulunuz.
Çözüm:
➡️ A ve B sayılarında ortak olan tabanlar 2 ve 3’dür.
➡️ Tabanı 2 olan ifadelerden üssü en az olan 23
➡️ Tabanı 3 olan ifadelerden üssü en az olan 31
➡️ Ortak tabanlardan üssü en küçük olanları bulduktan sonra EBOB’u bulmak için bu sayıları çarparız.
➡️ EBOB(A,B)= 23× 31
➡️ EBOB(A,B)=24
Örnek: Asal çarpanlara ayrılmış hali K = 32×53 ve L = 33×52×71 olan K ve L sayılarının en büyük ortak bölenini bulunuz.
Çözüm:
➡️ K ve L sayılarında ortak olan tabanlar 3 ve 5’dir.
➡️ Tabanı 3 olan ifadelerden üssü en az olan 32
➡️ Tabanı 5 olan ifadelerden üssü en az olan 52
➡️ Ortak tabanlardan üssü en küçük olanları bulduktan sonra EBOB’u bulmak için bu sayıları çarparız.
➡️ EBOB(A,B)= 32× 52
➡️ EBOB(K,L)=225
En Küçük Ortak Katı Bulma
Bilgi: İki ya da daha fazla doğal sayının ortak katlarının en küçüğüne bu sayıların en küçük ortak katı denir. En Küçük Ortak Katı kısaca EKOK şeklinde ifade ederiz.
✅ x ve y doğal sayılarının en küçük ortak katını EKOK(x,y) veya (x,y)ekok şeklinde gösterilir.
Örnek: 8 ve 12 sayılarının en küçük ortak katını bulalım.
➡️ Öncelikle 8 ve 12 sayılarının katlarını yazalım.
8 ‘in katları: 8,16,24,32,40,48,56,64,72,80,88,…..
12 ‘nin katları: 12,24,36,48,60,72,84,96,…….
➡️ 8 ve 12 ‘nin ortak katlarını yazalım
8 ve 12’nin ortak katları: 24,48,72,….
➡️ Bu ortak katların en küçüğüne EKOK denir.
8 ve 12’nin En Küçük Ortak Katı 24’dür.
Bunu EKOK(8,12)=24 veya (8,12)ekok =24 şeklinde ifade ederiz.
Örnek: 6 ve 9 sayılarının en küçük ortak katını bulalım.
➡️ Öncelikle 6 ve 9 sayılarının katlarını yazalım.
6 ‘nın katları: 6,12,18,24,30,36,42,48,54,60,…..
9 ‘un katları: 9,18,27,36,45,54,63,72,81,90,99,…….
➡️ 6 ve 9 ‘un ortak katlarını yazalım
8 ve 12’nin ortak katları: 18,36,54,….
➡️ Bu ortak katların en küçüğüne EKOK denir.
6 ve 9’un En Küçük Ortak Katı 18’dir.
Bunu EKOK(6,9)=18 veya (6,9)ekok =18 şeklinde ifade ederiz.
✅ Verilen sayıların en küçük ortak katını (EKOK) asal çarpan algoritması yöntemi ile bulabiliriz. Bu yöntemin adım adım açıklaması aşağıda verilmiştir.
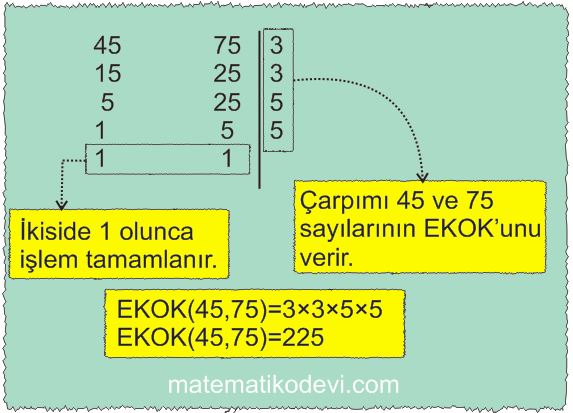
Örneğin 45 ve 75 sayısının en küçük ortak katını (EKOK) bulalım.
➡️ Bu yöntemde sayılar yan yana yazılarak bölen listesi yapılır ve sayılar bölünebilen en küçük asal sayıya bölünür. (sayılardan 1 tanesinin bölünmesi yeterli)

➡️ Bölünmeyen sayı aynen yazılır.

➡️ Sayılardan hiç biri ilk böldüğümüz asal sayıya bölünmüyorsa bir sonraki asal sayıya geçilir.

➡️ İki sayı da 1 olana kadar işleme devam edilir.

➡️ Sayıları bölen tüm asal sayıların çarpımı bu sayıların EKOK’u denir.
ÖRNEK: 36 ve 48 sayılarının EKOK’unu asal çarpanlar algoritması yöntemiyle bulalım.
ÇÖZÜM:

Not: Asal çarpanlarına ayrılmış olan pozitif tam sayıların EBOB ve EKOK’u aşağıdaki gibi bulabiliriz.
- Ortak olan tabanlardan üssü küçük olanları işaretle
- EBOB = Ortak olan asal çarpanlardan üssü küçük olanların çarpımı (İşaretli olanların çarpımı)
- EKOK = Ortak olan asal çarpanlardan üssü büyük olanlar ile ortak olmayan asal çarpanların çarpımı (İşaretli olmayanların çarpımı)

Örnek: Asal çarpanlara ayrılmış şekli K = 24×3×53 ve L = 22×33×52×7 olan K ve L sayılarının EBOB ve EKOK’unu bulalım.
✅ Ortak olan tabanlardan üssü küçük olanları işaretle (kırmızı renkle gösterilmiştir.)
K = 24×3×53
L = 22×33×52×7
✅ EBOB = Ortak olan asal çarpanlardan üssü küçük olanların çarpımı (İşaretli olanların çarpımı)
EBOB (K,L) = 22×3×52
✅ EKOK = Ortak olan asal çarpanlardan üssü büyük olanlar ile ortak olmayan asal çarpanların çarpımı (İşaretli olmayanların çarpımı)
EKOK (K,L) = 24×33×53×7
Not: Aralarında asal iki pozitif tam sayının EBOB’u 1’e, EKOK’u ise bu sayıların çarpımına eşittir.
a ve b aralarında asal ise;
✅ EBOB (a,b) = 1
✅ EKOK (a,b) = a×b
Örnek: 10 ve 27 sayılarını inceleyelim:
✅ 10 ve 27 sayıları aralarında asaldır.
Aralarında asal sayıların EBOB’u 1’e, EKOK’u ise bu iki sayının çarpımına eşittir.
EBOB(10,27) = 1
EKOK(10,27) = 10×27
EKOK(10,27) = 270
EBOB – EKOK PROBLEMLERİ
EBOB -EKOK sorularını çözmek için önce soruda sizden istenenin EBOB mu yoksa EKOK mu olduğuna karar vermelisiniz. Sizden istenenin EBOB mu yoksa EKOK mu olduğuna karar vermek için aşağıdaki yöntemleri kullanabilirsiniz.
✅ Eğer istenilene ulaşırken verilen sayıların katları kullanılacak ise EKOK kullanılır.
✅ Eğer istenilene ulaşırken verilen sayının bölenleri kullanılacak ise EBOB kullanılır.
✅ PARÇA verilip BÜTÜN isteniyor ise EKOK kullanılır.
✅ BÜTÜN verilip PARÇA isteniyor ise EBOB kullanılır.
EBOB SORULARINA ÖRNEKLER:
1) Bidonların, şişelerin, çuvalların, v.b. kapların içinde malzemeler verilip bu malzemelerin daha küçük ve eşit başka kaplara dağıtılması isteniyor ise (BÜTÜN verilip PARÇA isteniyor)
2) Arazinin (tarla, bahçe, arsa….) ölçüleri verilip etrafına eşit aralıklarla ağaç ,direk veya tel dikiliyorsa (İstenilene ulaşırken verilen sayının bölenleri kullanılıyor.)
3) Belirli gruplar verilip bu gruplar için kaç adet araç ( uçak, otobüs, araba…) veya otel odası gerekir diye soruluyor ise (BÜTÜN verilip PARÇA isteniyor)
4) Dikdörtgenler prizması şeklindeki odanın, kutunun, deponun ölçüleri verilip içine kaç küp sığar diye soruluyor ise (İstenilene ulaşırken verilen sayının bölenleri kullanılıyor.)
5) Kumaşlar, bezler, demir çubukların uzunlukları verilip eşit parçalara ayrılıyor ise (BÜTÜN verilip PARÇA isteniyor)
EKOK SORULARINA ÖRNEKLER:
1) Bademler, fındıklar, şekerler, bilyeler , cevizler ikişer-üçer-beşer vb. sayılıyor veya bunlar sayıldıktan sonra artan oluyor ise (istenilene ulaşırken verilen sayıların katları kullanılıyor.)
2) Bisikletler, motosikletler , arabalar, yarışçılar beraber yola çıkıp belirli bir zaman sonra bir yerde karşılaşıyor ise
3) Sınıfta öğrenciler sıralara ikişer-üçer-beşer vb. oturuyor ve ayakta kalan öğrenci oluyor ise
4) Ziller, saatler birlikte çaldıktan sonra tekrar birlikte ne zaman çalar diye soruluyor ise
5) Öğretmenler, doktorlar, hemşireler, eczacılar, işçiler birlikte nöbet tuttuktan sonra tekrar birlikte ne zaman nöbet tutarlar diye soruluyor ise (istenilene ulaşırken verilen sayıların katları kullanılıyor.)
Örnek: Hemşire olan Aslı 4 günde bir, Ece ise 6 günde bir nöbet tutmaktadır.
İkisi birlikte Salı günü nöbet tuttuktan sonra birlikte hangi gün nöbet tutarlar?
Çözüm:
EKOK (4 , 6) = 12 ➡️ 12 günde bir nöbet tutarlar.
Salı’dan sonraki ilk nöbet 12 gün sonra tutulur
12 gün sonra hangi gün olur bulalım.
Haftanın günleri 7 günde bir tekrar eder.
7.gün sonra yine Salı
14 gün sonra yine Salı
14 den geriye gidersek , 13 gün sonra pazartesi , 12 gün sonra pazar olur.
Örnek: 48 kg nohut ve 56 kg nohut hiç artmadan eşit hacimli çuvallara doldurulacaktır.
Bu iş için en az kaç çuval gereklidir?
Çözüm:
➡️ Bütün verilip eş parçalara ayrılacağı için EBOB kullanılır.
Az çuval kullanmak için çuvalın hacminin büyük olması gerekir.
➡️ EBOB (48, 56) = 8 kg (çuvalın hacmi)
➡️ 48 : 8 = 6 çuval
➡️ 56 : 8 = 7 çuval gerekir.
➡️ Toplam 13 çuval gereklidir.
Örnek: Fazıl şekerlerini üçer, beşer ve altışar saydığında her defasında 3 şekeri artıyor.
Buna göre, Fazıl’ın en az kaç tane şekeri vardır?
Çözüm:
➡️ Eğer şekerleri 3 eksik olsaydı şeker sayısı hem 3’ün, hem 5’in, hem de 6’nın katı olacaktı.
➡️ İstenilene ulaşırken verilen sayıların katları kullanıldığı için EKOK kullanılır.
➡️ 3,5 ve 6’nın en küçük ortak katını bulalım.
EKOK (3, 5, 6) = 30
➡️ 30 şekeri olsaydı şekerleri üçer, beşer ve altışar saydığında hiç şekeri artmazdı.
➡️ 3 şekeri artması için 30+3=33
➡️ 33 şekeri olursa şekerleri üçer, beşer ve altışar saydığında 3 şekeri artar.
Örnek: 100 cm ve 75 cm uzunluğunda iki kumaş hiç artmadan eşit uzunlukta parçalara ayrılacaktır.
Buna göre bir parçanın uzunluğu en fazla kaç cm olur?
Çözüm:
➡️ Bütün verilip eş parçalara ayrılacağı için EBOB kullanılır.
EBOB (100, 75) = 25
➡️ Her bir parça 25 cm olmalıdır.
EBOB – EKOK Test ve Etkinlik
Ebob- Ekok konusu ile ilgili test ve etkinlikleri aşağıdan çözebilirsiniz. İnternet hızından kaynaklı test ve etkinlikler açılmamış olursa sayfayı yenileyiniz.
🎥 Bir Soru Bir Video 🎥
Soru:
Aşağıda verilen kare ve eşkenar üçgen şeklindeki taşları ok yönünde kenarları üzerinde devirerek
kaydırmadan ilerletilecektir.

- Yağmur üçgen taşı her devirmesi 8 saniye ,
- Elif kare taşı her devirmesi 9 saniye sürmektedir.
Şekildeki konumda olan taşları Yamur ve Elif aynı anda başlayarak hiç durmadan devirmeye başlıyorlar.
Buna göre bu taşların aynı anda tekrar [NM] ve [BC] kenarları üzerinde yola temas
etmeleri için en az kaç saniye geçmelidir?
| A) 72 sn | B) 96 dn | C) 108 sn | D) 864 sn |
Çözüm:
🔻 Diğer konulara hızlı geçiş 🚀
| ⏪ Önceki Konu | Sonraki Konu ⏩ |
| Çarpanlar ve Asal Çarpanlar Konu Anlatımı | Aralarında Asal Sayılar Konu Anlatımı |

