Çarpanlar ve Asal Çarpanlar Konu Anlatımı
Çarpanlar ve Asal Çarpanlar Konu Anlatımı
Kazanım: Verilen pozitif tamsayıların çarpanlarını bulur; pozitif tamsayıları üslü ifade ya da üslü ifadelerin çarpımı şeklinde yazar.
Bu konuda neler öğreneceğiz :
Pozitif Tam Sayıların Pozitif Çarpanlarını Bulma
Çarpanlar ve Asal Çarpanlar Konu Anlatımına pozitif tam sayıların pozitif çarpanlarını yani bölenlerini bularak başlayacağız.
Bilgi: Pozitif tam sayıyı kalansız olarak bölen sayılara o sayının çarpanı yada böleni denir.
Çarpan=Bölen
✅ 24 sayınını 2 sayısı böler. Bundan dolayı➡️2 sayısı 24 sayısının çarpanıdır. (bölenidir)
✅ 24 sayınını 5 sayısı bölmez Bundan dolayı➡️ 5 sayısı 24 sayısının çarpanı değildir. (böleni değildir.)
✅ Bir sayının çarpanlarını bulmak için bölünebilme kurallarını iyi biliyor olmamız lazım. Aşağıda verilen bölünebilme kurallarını inceleyerek kuralları tekrar hatırlayalım.

✅ Verilen bir sayının çarpanlarını bulmak için verilen sayıyı iki sayının çarpımı şeklinde yazarak bulabiliriz.
ÖRNEK: 30 sayısının pozitif çarpanlarını (bölenlerini) bulalım.
➡ 30 sayısını iki sayının çarpımı şeklinde yazalım.
1×30
2×15
3×10
5×6
6×5 (aynısını yukarıda yazdık)
➡ 30 sayısının çarpanları (bölenleri) = 1,2,3,5,6,10,15,30
ÖRNEK: 48 sayısının pozitif çarpanlarını (bölenlerini) bulalım.
➡ 48 sayısını iki sayının çarpımı şeklinde yazalım.
1×48
2×24
3×16
4×12
6×8
8×6 (aynısını yukarıda yazdık)
➡ 48 sayısının çarpanları (bölenleri) = 1,2,3,4,6,8,12,16,24,48
Not: Bir pozitif tam sayının çarpanlarının sayısı en az 2 tane olmak zorundadır. (1 ve kendisi)
✅ Bir sayının kendisinden büyük çarpanı hiçbir zaman olmaz.
✅ Bir sayının En küçük çarpanı her zaman 1 olur.
Bilgi: Dikdörtgenin alanı verilip kenarlarının alabileceği tam sayı değerleri sorulduğunda verilen alanın çarpanlarını (bölenlerini) bulmamız gerekir.
Örnek: Alanı 50 cm2 olan dikdörtgenin kenarlarının alabileceği tam sayı değerlerini bulunuz.
➡ Alanı 50 cm2 ise kenarları 50 ‘nin çarpanları olabilir.
➡ 50 sayısının çarpanlarını yazalım.
1×50
2×25
5×10
➡ 50 sayısının çarpanları (bölenleri) = 1,2,5,10,25,50
➡ Dikdörgenin kenarları = 1 cm ve 50 cm ,2 cm ve 25 cm ,5 cm ve 10 cm olabilir.
Bilgi: Verilen pozitif tam sayı bir tam sayının karesi ise tek sayı adedince pozitif çarpanı , bir tam sayının karesi değil ise çift sayı adedince pozitif çarpanı vardır.

ÖRNEK: Aşağıda verilen sayıların pozitif çarpanlarının sayısının tek mi çift mi olduğunu bulalım.
➡ 25
25 sayısı 5 ‘in karesi olduğu için tek adet çarpanı vardır.
➡ 30
30 sayısı bir sayının karesi olmadığı için çift adet çarpanı vardır.
➡ 36
36 sayısı 6 ‘nın karesi olduğu için tek adet çarpanı vardır.
➡ 40
40 sayısı bir sayının karesi olmadığı için çift adet çarpanı vardır.
Bilgi: Verilen bir pozitif tam sayının çarpanlarını küçükten büyüğe doğru sıralı bir şekilde yazdığımızda ;
✅ en baştaki ve en sondaki çarpanların çarpımı
✅ baştan ikinci sıradaki ve sondan ikinci sıradaki çarpanların çarpımı
✅ baştan üçüncü sıradaki ve sondan üçüncü sıradaki çarpanların çarpımı …… verilen pozitif tam sayıyı vermelidir. Bu yönteme gökkuşağı yöntemi denir. Bu yöntemle verilen bir pozitif sayının çarpanlarını doğru bulup bulmadığımızı anlarız.

Pozitif Tam Sayıların Asal Çarpanlarını Bulma
Asal Sayılar
Bilgi: Pozitif çarpanları (bölenleri) sadece 1 ve kendisi olan 1’den büyük sayılara asal sayılar denir.
✅ 2,3,5,7,11,13,17,19,23…….. gibi sayılar asal sayılardır.
✅ En küçük asal sayı 2
✅ Asal sayılar arasında 2 ‘den başka çift asal sayı yoktur.
Eratosthenes (Eratostenes) asal sayıları bulmak için basit bir yöntem geliştirmiştir. Bu yöntem Eratosthenes (Eratostenes) kalburu olarak bilinir.
Eratosthenes (Eratostenes) kalburu yöntemİ ile 120 ye kadar olan asal sayıları bulmak için aşağıdaki basamakları takip ediniz.
- 1 asal sayı olmadığı için çarpı işareti koyun.
- 2 asal sayı olduğu için daire içine alın ve katlarına da çarpı işareti koyun.
- 3 asal sayı olduğu daire içine alın ve katlarına da çarpı işareti koyun.
- 5 asal sayı olduğu daire içine alın ve katlarına da çarpı işareti koyun.
- 7 asal sayı olduğu daire içine alın ve katlarına da çarpı işareti koyun.
- Geriye kalan sayıları yuvarlak içine alın
- Yuvarlak içine alınan sayılar 120 ‘ ye kadar olan asal sayılardır.
120′ye kadar olan tüm sayılara bu işlemi uygularsanız, 120′ye kadar olan asal sayıları aşağıdaki gibi bulursunuz.

Asal Çarpanlara Ayırma
Bir pozitif tam sayının asal sayıların çarpımı şeklinde yazılmasına , asal çarpanlara ayırma adı verilir.
✅ 45 sayısının asal çarpanlara ayrılmış hali 3 × 3 × 5 ‘dir
Pozitif sayıların asal çarpanları çarpan ağacı ve asal çarpan algoritması yöntemlerini kullanarak bulunur.
1) Çarpan Ağacı
Bir sayıyı asal çarpanlarına ayırmak için çarpan ağacı yöntemini kullanabiliriz. Bu yönteme göre bir sayıyı biri en küçük asal sayı olmak üzere iki sayının çarpımı şeklinde yazarız. ( 1 hariç) Sayılar yazılırken ağaç dalları gibi ikiye ayrılır. En son adımda bütün sayılar asal sayı olunca çarpan ağacımız tamamlanmış olur. Çarpan ağacında dalların uçlarındaki asal sayıların çarpımı, çarpanlarına ayırdığımız sayıyı verir.
✅ Aşağıda verilen şekilde 20 sayısının çarpan ağacı yöntemine göre çarpanlara ayrılmış hali gösterilmiştir.
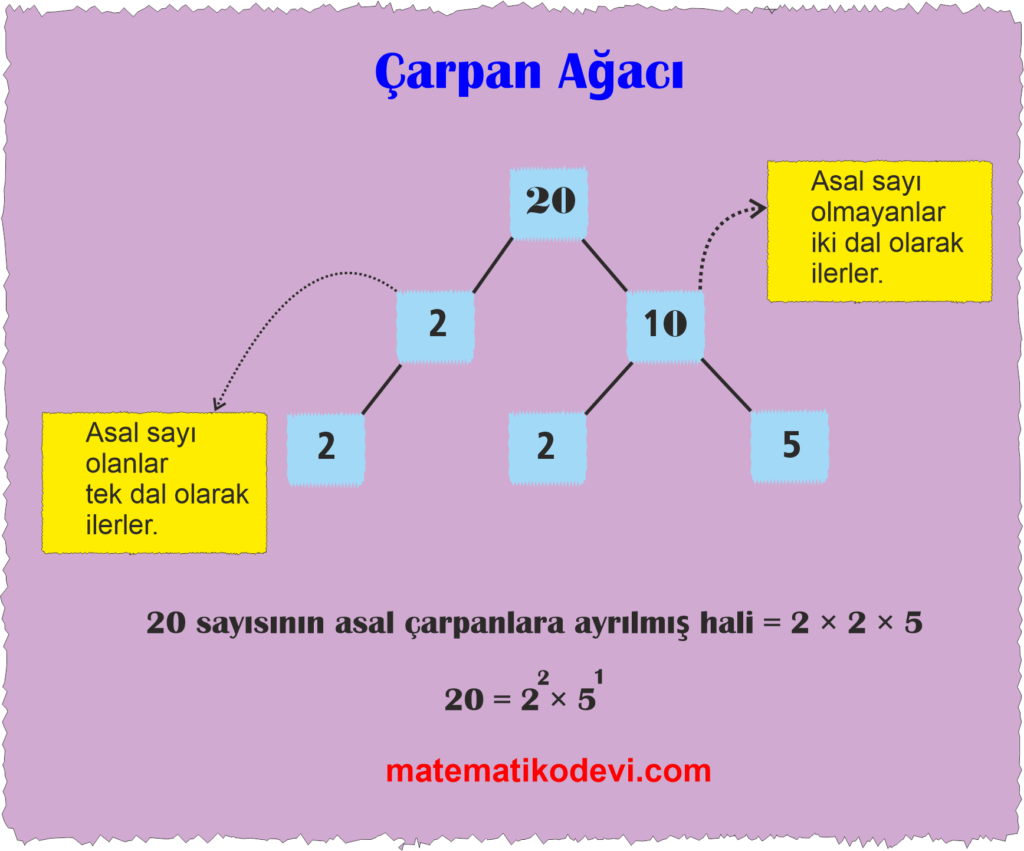

2) Asal Çarpan Algoritması (Bölen Listesi)
Asal Çarpan Algoritması diğer adıyla Bölen listesi aşağıdaki adımlar takip edilerek yapılır.
- Asal çarpanlarına ayıracağımız sayının yanına dikey bir çizgi çekeriz.
- Asal çarpanlarına ayıracağımız sayıyı en küçük asal sayıdan başlayarak ve tam bölünmediğinde bir sonraki asal sayıya geçerek bölme işlemi yaparız.
- Asal çarpanlarına ayıracağımız sayıda 1’i elde edince işlemimiz sona erer.
- Çizginin sağında kalan sayılar asal çarpanlarına ayırdığımız sayının asal çarpanlarıdır.,

Pozitif Tam Sayıların Asal Çarpanlarını Üslü İfade Şeklinde Yazma
Bilgi: Verilen bir pozitif tam sayıyı asal çarpanlara ayırdıktan sonra çarpım durumundaki sayıları üslü sayı olarak ifade edilmesine pozitif tam sayıların asal çarpanlarını üslü ifade şeklinde yazma denir.
✅ 200 sayısının asal çarpanlara ayıralım.
2× 2 × 2 × 5 × 5
✅ Asal çarpanları üslü olarak yazalım.
23×52
Örnek: 48 sayısının asal çarpanlara ayrılmış halini , asal çarpanlarını ve asal çarpanların üslü olarak yazılmış halini asal çarpan algoritması yöntemine göre bulalım.

Örnek: 72 sayısının asal çarpanlara ayrılmış halini , asal çarpanlarını ve asal çarpanların üslü olarak yazılmış halini çarpan ağacı yöntemine göre bulalım.

✅ Asal çarpan algoritması yönteminde verilmeyen harfleri bulurken sayıları 1 ‘ den başlayıp çapraz olarak çarparız.

✅ Çarpan ağacı yönteminde verilmeyen harfleri bulurken dalların ucundaki kutuların çarpımı üst kısmındaki kutunun değerini verir.Eğer dallar tek dal olarak ilerliyorsa bu kutudaki sayıların asal sayılar olduğunu gösterir ve üsteki kutu ile aynı değere sahip olur.

Not: 1 sayısının 1 tane çarpanı vardır. ( 1 sayısı)
1 sayısı asal olmadığından 1 sayısının asal çarpanları toplamı sıfırdır.
Çarpanlar ve Asal Çarpanlar Test
Çarpanlar ve Asal Çarpanlar konusu ile ilgili aşağıda test ve etkinliği çözerek konuyu pekiştirebilirsiniz. İnternet hızınız kaynaklı test ve etkinlik açılmamış olursa sayfayı yenileyiniz.
🎥 Bir Soru Bir Video 🎥
Soru:
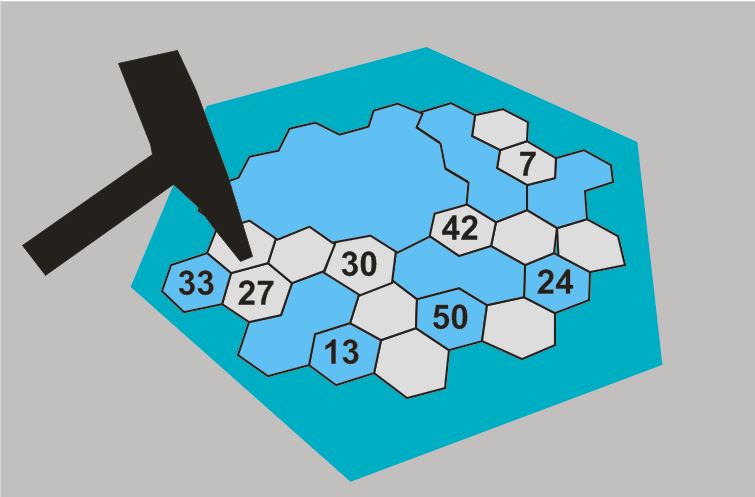
Buz tuzağı oyunu 2 oyuncunun sıra ile buz küplerine birer vuruş yaparak küpü düşürmesi ile oynanan bir oyundur.
Buz tuzağı oyununda oyuncuların kaç puan aldığı hesaplamak için bazı küplerin üzerine sayılar yazılmıştır.
Küplerin üzerindeki sayılar ;
Asal sayı ise üzerinde yazan sayının değeri kadar puan alır.
Asal sayı değil ise en büyük asal çarpanının değeri kadar puan alır.
Hatice Kübra bu oyundan 27 puan aldığına göre aşağıdaki sayısı verilen küplerden hangisini kesinlikle düşürmüştür?
| A) 24,33,50 | B) 13,27,42 | C) 7,24,30 | D) 13,27,33 |
Çözüm:
🔻 Diğer konulara hızlı geçiş 🚀
| ⏪ Önceki Konu | Sonraki Konu ⏩ |
| EBOB (En Büyük Ortak Bölen) – EKOK (En Küçük Ortak Kat) Konu Anlatımı |

