Basit Cebirsel İfadeler Konu Anlatımı
Kazanım: Basit cebirsel ifadeleri anlar ve farklı biçimlerde yazar.
Bu konuda neler öğreneceğiz :
BASİT CEBİRSEL İFADELER
CEBİRSEL İFADE VE BİLİNMEYEN NEDİR?
Bilgi: En az bir bir bilinmeyen ve bir işlem içeren ifadelere cebirsel ifadeler denir. Cebirsel ifadelerde sayıları temsil eden Cebirsel ifadelerde x, y, z, m, n ve k gibi kullanılan harflere değişken ya da bilinmeyen denir.

Örnek: Ayşe 30 yaşındadır.Ayşe’nin yaşının 3 katının 10 eksiği ifadesi cebirsel ifade belirtir mi inceleyelim.
➡ Ayşe 30 yaşındadır ifadesinden dolayı bu ifadede bilinmeyen yoktur.
➡ İçinde bilinmeyen olmayan ifadeler cebirsel ifade değildir.
TERİM NEDİR?
Bilgi: Bir cebirsel ifadede “+” veya “–” işaretleriyle ayrılan kısımlara terim denir.
Örnek: 3x+2y-7 cebirsel ifadesinin terimlerini bulalım.
➡ 3x+2y-7 ifadesinde ➕ ve ➖ işaretlerinin sol tarafından aşağıdaki gibi ayıralım.
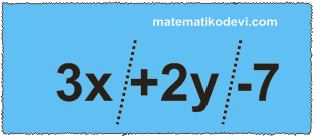
➡ Elde ettiğimiz her bir ifade terimdir.
➡ 3x+2y-7 cebirsel ifadesinin terimleri 3x , 2y ve -7’dir.
SABİT TERİM VE KATSAYI NEDİR?
Bilgi: Her bir terimin sayısal çarpanına, katsayı denir.
Bilgi: Hiçbir değişkene bağlı olmayan terime, sabit terim denir.
✅ Sabit terim de cebirsel ifadenin bir katsayısıdır.
Örnek: 5a-2b+12 cebirsel ifadesinin katsayılarını ve sabit terimini bulalım.
➡ 5a-2b+12 cebirsel ifadesinin önce terimleri 5a , -2b ve 12 ‘dir.
➡ Terimlerin değişkeni ile çarpım durumunda olan sayılar katsayısıdır.
➡ 5a teriminde a değişkeniyle çarpım durumunda olan 5 katsayı dır.
➡ -2b teriminde b değişkeniyle çarpım durumunda olan (-2) katsayı dır.
➡ Değişkeni olmayan 12 sabit terimdir.
➡ Sabit terimde katsayı olduğu için 12 katsayı dır.
➡ 5a-2b+12 cebirsel ifadesinin katsayıları 5 , (-2) ve 12 ‘dir.
Örnek: Aşağıda verilen cebirsel ifadelerin terimlerini,değişkenlerini,katsayılarını ve sabit terimini bulunuz.
✅ 8x2 – 5x
Terimleri: 8x2 ve – 5x
Değişkenleri: x
Katsayıları: 8 ve -5
Sabit Terim: 0
✅ 4a2 – 6b-11
Terimleri: 4a2 , (- 6b) ve -11
Değişkenleri: a ve b
Katsayıları: 4 ,-6 ve -11
Sabit Terim: -11
✅ 6m2 – bc +2
Terimleri: 6m2 , -bc ve 2
Değişkenleri: m,b ve c
Katsayıları: 6,-1 ve 2
Sabit Terim: 2

BENZER TERİM NEDİR?
Bilgi: Hem değişkeni hem de değişkene ait kuvveti aynı olan terimlere benzer terim denir. Benzer terimler, kendi aralarında toplama veya çıkarma işlemi yapılabilir.
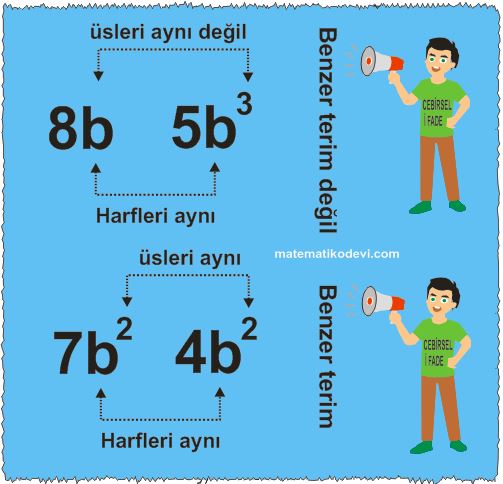
Örnek: 5a2 + 7a – 8a2 + 4a Cebirsel ifadesinde benzer terimleri bulalım.
➡ 5a2 ve 7a terimlerinin değişkenleri aynı (ikisinde de a) ama değişkenlerinin kuvvetleri aynı değil (Birinde a’nın kuvveti 1 , diğerinde ise a’nın kuvveti 2)
➡ 5a2 ve 7a terimleri benzer terim değildir.
➡ 5a2 ve – 8a2 terimlerinin hem değişkenleri aynı hemde hemde değişkenlerin kuvvetleri aynı
➡ 5a2 ve – 8a2 terimleri benzer terimdir.
➡ 7a ve 4a terimlerinin hem değişkenleri aynı hemde hemde değişkenlerin kuvvetleri aynı
➡ 7a ve 4a terimleri benzer terimdir.

Not: Sorularda fazlası derse + kullanılır , eksiği derse – kullanılır , katı derse × kullanılır , yarısı derse ½ ile çarpılır.
Örnek: Aşağıda verilen ifadeleri cebirsel ifade olarak yazalım.
✅ Ali’nin parasının 2 katının 3 eksiği ➡ 2a-3
✅ Ali’nin parasının 6 katının 2 eksiğinin yarısı ➡ \dfrac{6a-2}{2}
✅ Ali’nin parasının 4 eksiğinin 5 katı ➡ 5×(a-4)
✅ Ali’nin parasının 2 eksiğinin 8 katının 3’te biri ➡ \dfrac{8(a-2)}{3}
Basit Cebirsel İfadeler Doğru Yanlış Testi
Yeni Nesil Soru
🎥 Bir Soru Bir Video 🎥
Soru: Bir bilgisayar programına yazılan kod aşağıdaki gibi çalışmaktadır.
dıv[(cebirsel ifade)]= \dfrac{ cebirsel \ ifadenin \ katsayıları \ toplamı}{ sabit \ terim}
ltx[(cebirsel ifade)]= cebirsel ifadenin terim sayısı cebirsel ifadenin en büyük katsayısı

Örneğin aşağıda yazılan kodların değeri
dıv[(3x3-7x+1)]= \dfrac{ -3}{ 1} =-3
ltx[( 2x3-7x+1 )]= 32 =9 şeklinde bulunur.
Kaan bu bilgisayar programına aşağıdaki gibi kod yazmıştır.
dıv[(4a3+2a-9x-3)] + ltx[( 2b4-7x-3b-2m+1 )]
Buna göre Kaan’ın yazdığı kodun değeri aşağıdakilerden hangisidir?
| A) 25 | B) 26 | C) 27 | D) 28 |
Çözüm:
🔻 Diğer konulara hızlı geçiş 🚀
| ⏪ Önceki Konu | Sonraki Konu ⏩ |
| Cebirsel İfadelerde Çarpma İşlemi |

