Üçgenlerde Eşlik ve Benzerlik Konu Anlatımı
Kazanım: Eşlik ve benzerliği ilişkilendirir, eş ve benzer şekillerin kenar ve açı ilişkilerini belirler.
Üçgenlerde Eşlik ve Benzerlik Konu Anlatımını iki üçgenin açı ve kenarlarının birbirine eşit olmasını (eşlik) ve iki üçgenin açıları birbirine eşit ve kenar uzunlukları orantılı olmasını (benzerlik) inceleyeceğiz.
Bu konuda neler öğreneceğiz :
Üçgenlerde Eşlik
Bilgi: Bir üçgenin karşılıklı açılarının ölçüleri ve bu açılarının karşısındaki kenarlarının uzunlukları eşit ise bu üçgene eş üçgen denir.
✅ İki üçgenin eşliği “≅” sembolü ile gösterilir.
✅ ABC üçgeni ile DEF üçgeni eş ise ABC≅DEF şeklinde gösterilir.
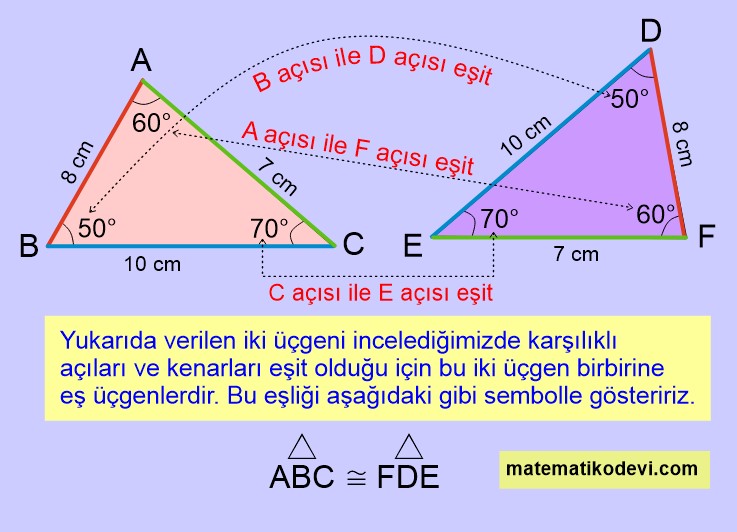
👉🏻 Yukarıdaki görselde verilen iki üçgenin eşit açılarını yazalım.
\textstyle\widehat{A} = \textstyle\widehat{F} = 60°
\textstyle\widehat{B} = \textstyle\widehat{D} = 50°
\textstyle\widehat{C} = \textstyle\widehat{E} = 70°
🙄 Eşit açıları sıralı bir şekilde yazdığımızda ABC üçgeni ile FDE üçgeninin eş olduğunu görürüz. Bunu aşağıdaki gibi gösteririz.
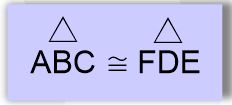
👉 Yukarıdaki görselde verilen iki üçgenin eşit olan kenarlarını yazalım.
|AB| = |FD| = 8 cm
|BC| = |DE| = 10 cm
|AC| = |FE| = 7 cm
Not: İki üçgenin eşliğini yazarken ölçüleri aynı olan açıların aynı sırada yazılmalıdır.
✅ Örneğin A açısı ile F açısı eşit ise A açısını birinci sırada yazdığımızda F açısını da birinci sırada yazmalıyız.
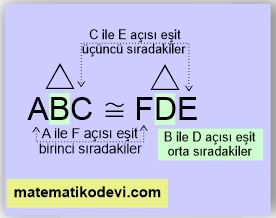
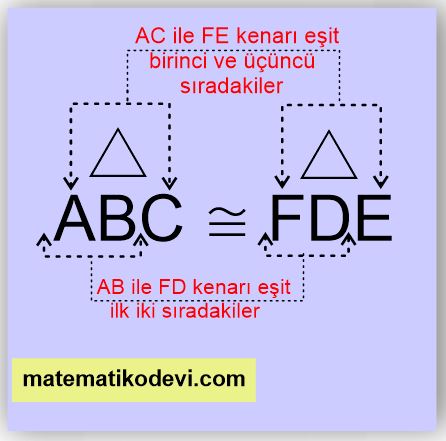
Not: İki üçgenin eşliği verildiğinde sıralı bir şekilde kenar uzunlukları birbirine eşittir.
✅ Örneğin ABC üçgeni ile FDE üçgeni birbirine eş ise ilk iki sıradaki AB kenarı ile FD kenarı birbirine eşittir.
Örnek:
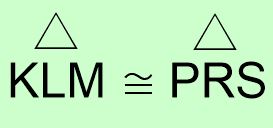
Yukarıda verilen eşliğe göre eşit olan açıları ve eşit olan kenarları yazalım.
👉 Eşit olan açılar ⤵
\textstyle\widehat{K} = \textstyle\widehat{P}
\textstyle\widehat{L} = \textstyle\widehat{R}
\textstyle\widehat{M} = \textstyle\widehat{S}
👉 Eşit olan kenarlar ⤵
|KL| = |PR|
|LM| = |RS|
|KM| = |PS|
Üçgenlerde Eşlik Şartları
İki üçgenin karşılıklı tüm kenarlarının uzunlukları ve tüm açılarının ölçüleri eşitse bu iki üçgenin birbirine eş olduğunu yukarıda anlattık. Ancak iki üçgenin tüm kenarları ve tüm açıları her zaman sorularda verilmeyebilir. Böyle durumlarda verilen bilgilere bakarak iki üçgenin eş olup olmadığına karar verebiliriz. Bunun için aşağıda verilen başlıklardaki eşlik şartlarını kullanırız. Eğer iki üçgen arasında aşağıda verilen şartlardan biri sağlanıyorsa bu iki üçgen birbirine eştir diyebiliriz.
1) Kenar-Kenar-Kenar Eşlik Şartı (KKK)
Bilgi: İki üçgen karşılaştırıldığında karşılıklı kenarları uzunlukları birbirine eşit ise bu iki üçgen birbirine eştir diyebiliriz. Bu yönteme kenar-kenar-kenar (KKK) eşliği denir.
Örneğin;
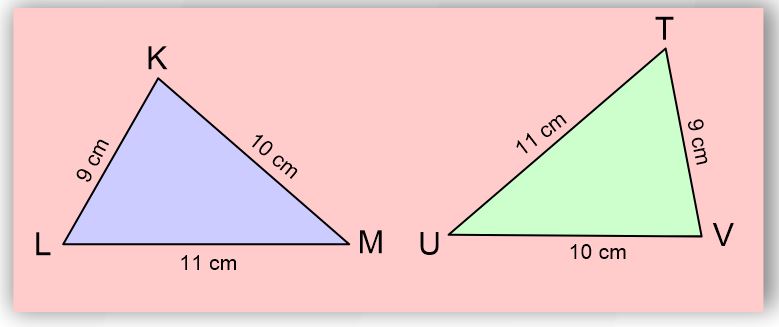
Yukarıda verilen iki üçgeninin kenarlarını inceleyelim.
|KL| = |TV| = 9 cm
|KM| = |UV| = 10 cm
|LM| = |TU| = 11 cm
🤓 Yukarıda verilen iki üçgeni karşılaştırdığımızda karşılıklı kenarlarının eş olduğunu bulduk. Bu durumda bu iki üçgen arasında kenar kenar kenar eşliği vardır diyebiliriz. Ama bu eşliği yazarken doğru sırayla yazmamız lazım.
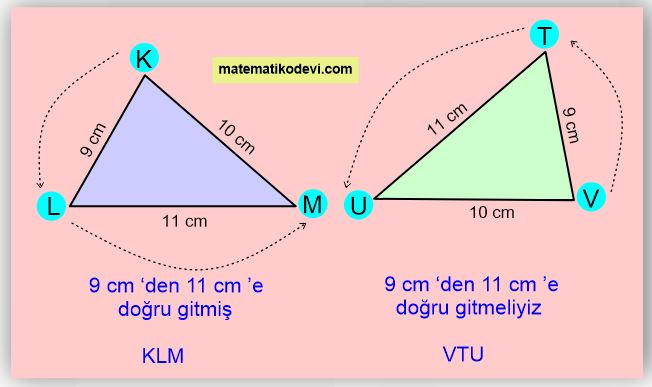
🤓 Yukarıda verilen görsele göre sıralamaya dikkat ederek Kenar Kenar Kenar üçgen eşliğini aşağıdaki gibi yazarız.

Not: Kareli zeminde verilen üçgenlerin kenarlarının eşit olup olmadığını belirlemek için kareleri sayarız. Kareli zeminde eğik olarak verilen kenarları hesaplamak için eğik kenar hipotenüs olacak şekilde Pisagor bağıntısını kullanırız.
Örnek:
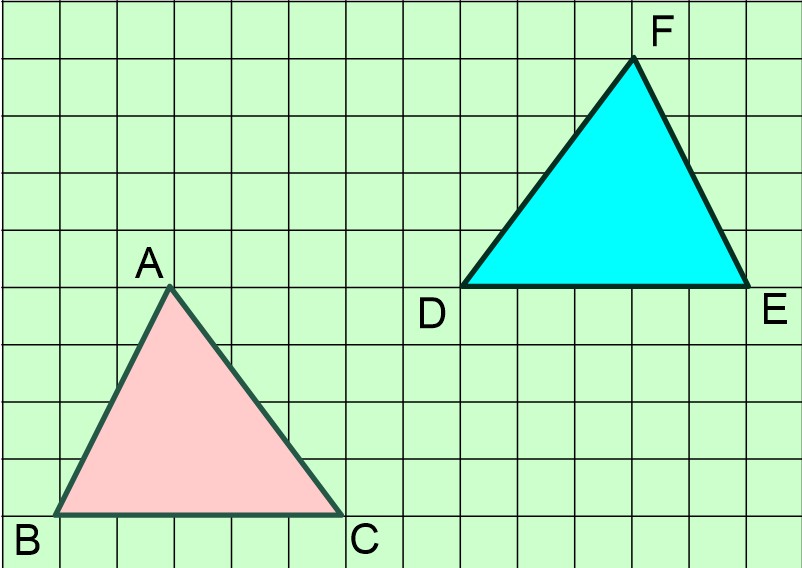
Yukarıda kareli zeminde verilen ABC ve DEF üçgenleri bir birine eş mi bulalım?
👉 Eğik olan AC ve FD kenarları hipotenüs olacak şekilde dik üçgen oluşturalım.
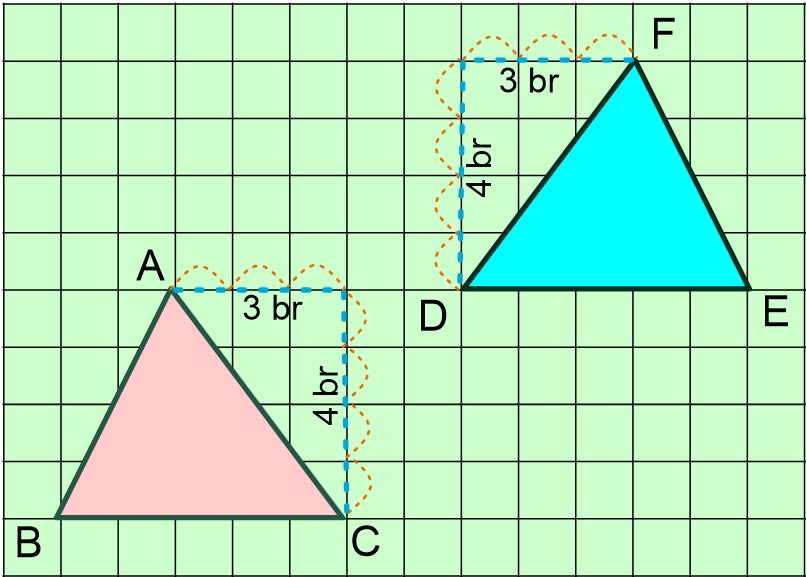
AC kenarında oluşan dik üçgen 3-4-5 dik üçgenidir. |AC| = 5 br olur.
DF kenarında oluşan dik üçgen 3-4-5 dik üçgenidir. |DF| = 5 br olur.
|AC| = |DF| olur.
👉 Eğik olan AB ve FE kenarları hipotenüs olacak şekilde dik üçgen oluşturalım.
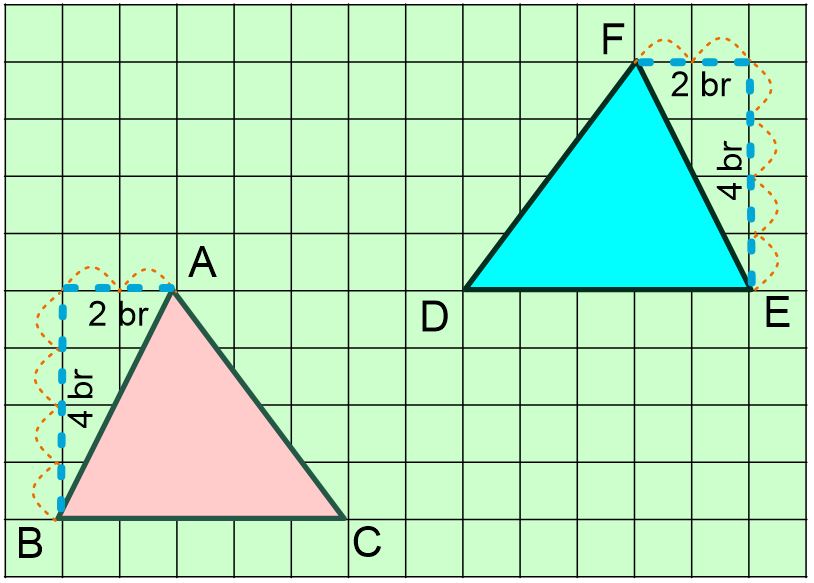
AB kenarında oluşan dik üçgen 22 + 42 = |AB|2
|AB|2 = 4+16
|AB|2 = 20
|AB|= \sqrt {20 } br
FE kenarında oluşan dik üçgen 22 + 42 = |FE|2
|FE|2 = 4+16
|FE|2 = 20
|FE|= \sqrt {20 } br
|AB| = |FE| olur.
👉 BC ve DE kenarlarını saydığımızda ikiside 5 br ‘dir.
|BC| = |DE| olur.
ABC ve DEF üçgenini karşılaştırdığımızda karşılıklı kenar uzunluklarının eşit olduğunu bulduk. Bu durumda bu iki üçgen birbirine eş üçgenlerdir. Bu eşitliği eşit olan kenarlar sıralı olacak şekilde aşağıdaki gibi yazarız.
ABC ≅ FED
2) Kenar – Açı – Kenar Eşlik Şartı (KAK)
Bilgi: İki üçgen karşılaştırıldığında ikişer kenar uzunlukları ve bu iki kenar arasında kalan açılarının ölçüleri eşit ise bu iki üçgen birbirine eş üçgenlerdir. Bu eşliğe Kenar – Açı – Kenar (KAK) eşlik şartı denir.
Örneğin;
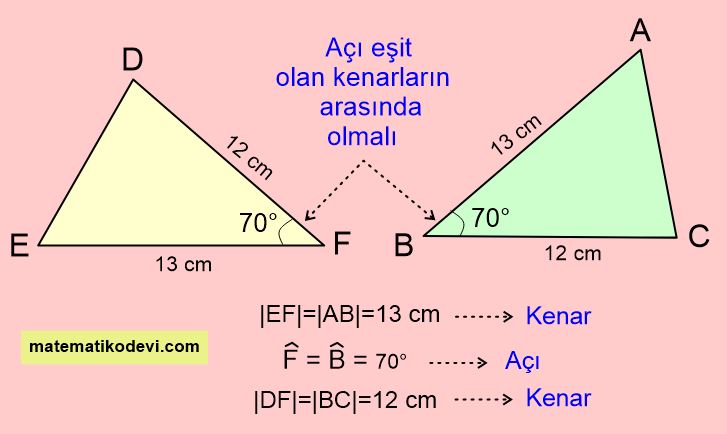
Yukarıdaki görselde verilen DEF ve ABC üçgenlerini incelediğimizde iki kenarı ve bu iki kenarın arasında kalan açının eşit olduğunu görürüz. Bu durumda bu iki üçgen arasında Kenar-Açı-Kenar (KAK) eşliği vardır denir. Şimdi bu eşliği nasıl yazacağımızı aşağıdaki görseli inceleyerek öğrenelim.
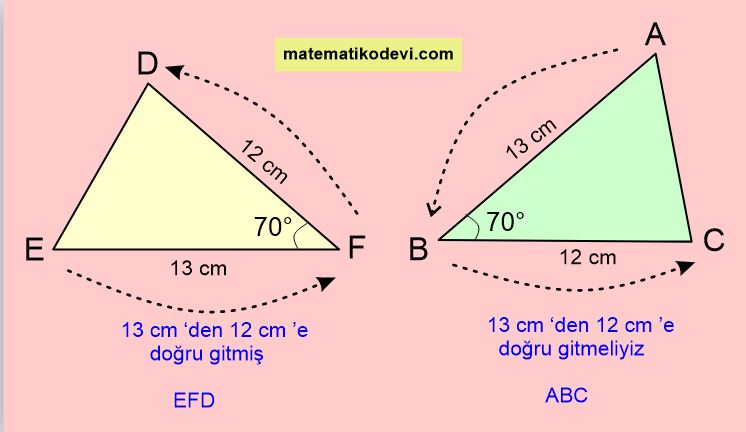
Bu eşliği yazarken yukarıda verilen görseldeki gibi sıraya dikkat ederek yazarız.
EFD ≅ ABC
3) Açı – Kenar – Açı Eşlik Şartı (AKA)
Bilgi: İki üçgen arasında birebir eşleme yapıldığında ikişer açılarının ölçüleri ve bu iki açı arasında kalan kenar uzunlukları eşit ise bu üçgenler birbirine eş üçgenlerdir. Bu eşliğe Açı – Kenar – Açı (AKA) eşlik şartı denir.
Örneğin;
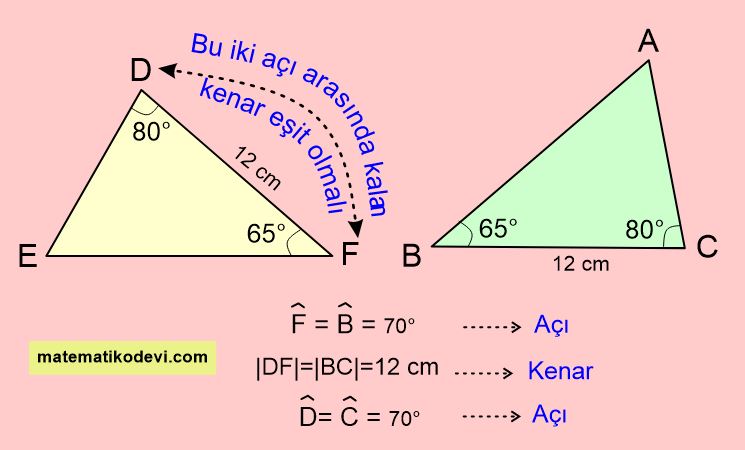
Yukarıdaki görselde verilen DEF ve ABC üçgenlerini incelediğimizde iki açısı ve bu iki açının arasında kalan kenarının eşit olduğunu görürüz. Bu durumda bu iki üçgen arasında Açı-Kenar-Açı (AKA) eşliği vardır denir. Şimdi bu eşliği nasıl yazacağımızı aşağıdaki görseli inceleyerek öğrenelim.
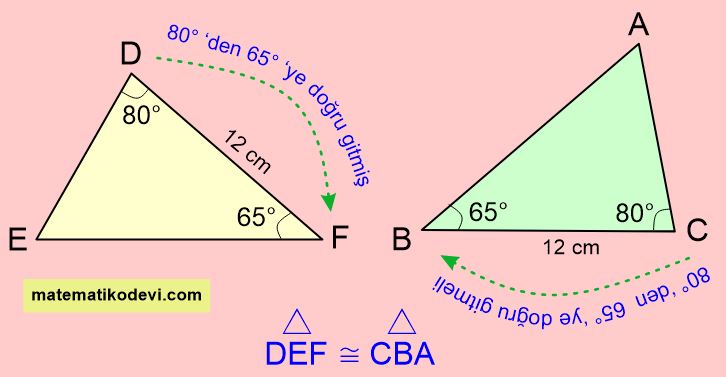
Bu eşliği yazarken yukarıda verilen görseldeki gibi sıraya dikkat ederek yazarız.
DEF ≅ CBA
4) Kenar – Açı – Açı Eşlik Şartı (KAA)
Bilgi: İki üçgen arasında birebir eşleme yapıldığında ikişer açılarının ölçüleri ve bu açılardan herhangi birinin karşısındaki kenarın uzunlukları eşit ise bu üçgenler birbirine eş üçgenlerdir. Bu eşliğe Kenar – Açı – Açı (KAA) eşlik şartı denir.
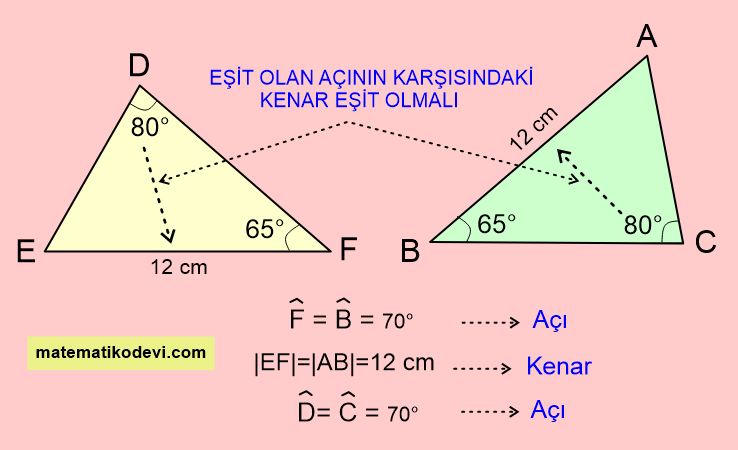
Yukarıdaki görselde verilen DEF ve ABC üçgenlerini incelediğimizde iki açısı ve bu iki açının karşısındaki kenarın eşit olduğunu görürüz. Bu durumda bu iki üçgen arasında Kenar-Açı-Açı (KAA) eşliği vardır denir. Şimdi bu eşliği nasıl yazacağımızı aşağıdaki görseli inceleyerek öğrenelim.

Bu eşliği yazarken yukarıda verilen görseldeki gibi sıraya dikkat ederek yazarız.
DEF ≅ CBA
ÜÇGENLERDE BENZERLİK
Bilgi: İki üçgenin karşılıklı açılarının ölçüleri birbirine eşit ve eş olan açıların karşısındaki kenarlarının uzunlukları orantılı ise bu iki üçgen birbirine benzer üçgenlerdir.
📌 İki üçgenin benzerliği “∼” sembolü ile gösterilir. Sembolle gösterirken eş olan açılar aynı sırada olacak şekilde yazılmalıyız. Örneğin ABC üçgeni ile DEF üçgeni benzer ise bu benzerliği ABC∼DEF şeklinde gösteririz.
📌 Benzer iki üçgende karşılıklı kenarları oranlarsak bu oranlar bir sayıya eşit olur. Bu sayıya benzerlik oranı denir. Genelde k harfi ile gösterilir.
Örnek:
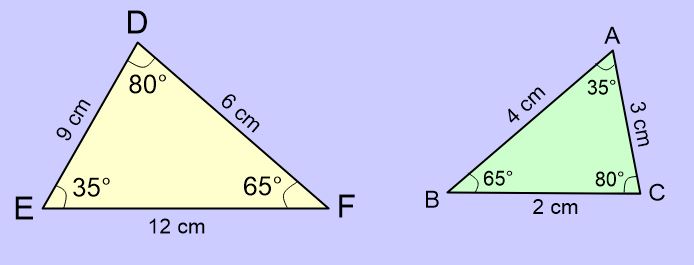
Yukarıdaki görselde verilen üçgenin benzer olup olmadığını inceleyelim.
👉 Karşılıklı açıların ölçüleri birbirine eşit olmalı
\textstyle\widehat{D} = \textstyle\widehat{C}
\textstyle\widehat{E} = \textstyle\widehat{A}
\textstyle\widehat{F} = \textstyle\widehat{B}
👉 Eş olan açıların karşısındaki kenarlarının uzunlukları orantılı olmalı
\dfrac{DE}{AC} = \dfrac{9}{3} = \dfrac{3}{1}
\dfrac{EF}{AB} = \dfrac{12}{4} = \dfrac{3}{1}
\dfrac{DF}{BC} = \dfrac{6}{2} = \dfrac{3}{1}
🤓 İki üçgeni karşılaştırdığımızda karşılıklı açıların ölçüleri eşit ve eşit olan aşıların karşısındaki açılar orantılı olduğu için bu iki üçgen benzerdir.
🤓 Bu iki üçgenin benzerlik oranı \dfrac{3}{1} ‘dir.
ÜÇGENLERDE BENZERLİK ŞARTLARI
İki üçgenin benzer olup olmadığını anlamak için her zaman tüm kenarları ve tüm açıları verilmeyebilir. Böyle durumlarda verilen bilgililere bakarak iki üçgenin benzer olup olmadığına karar verebiliriz. Bunun için aşağıdaki benzerlik şartlarını kullanırız. Eğer iki üçgen arasında bu şartlardan biri sağlanıyorsa bu iki üçgen benzerdir diyebiliriz.İki üçgenin benzerliği “∼” sembolü ile gösterilir.
1) Kenar – Kenar – Kenar Benzerlik Şartı (KKK)
Bilgi: İki üçgen arasında birebir eşleme yapıldığında karşılıklı kenar uzunluklarının oranı birbirine eşit ise bu üçgenler benzer üçgenlerdir. Bu benzerliğe Kenar – Kenar – Kenar (KKK) benzerlik şartı denir.
Örneğin;
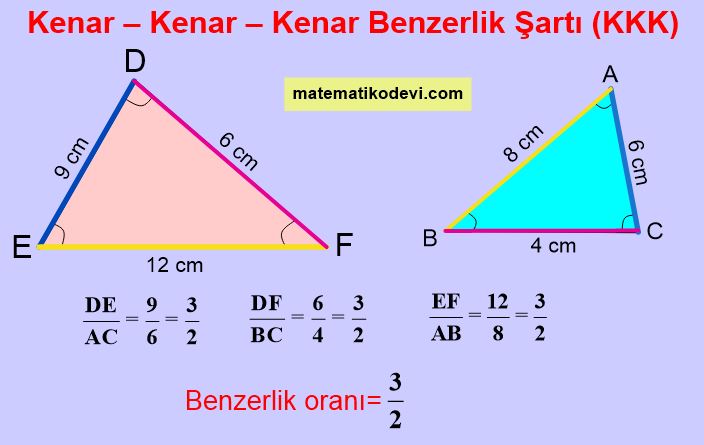
Yukarıda verilen iki üçgenin kenar uzunluklarını oranladığımızda oranlarının birbirine eşit olduğunu görürüz. Bu durumda bu iki üçgen arasında Kenar-Kenar-Kenar benzerliği vardır denir. Bu benzerliği yazarken sıraya dikkat ederek yazmalıyız.
🤓 Kenar-Kenar-Kenar benzerliğini doğru sırayla yazmak için aşağıdaki yöntemi kullanabiliriz.
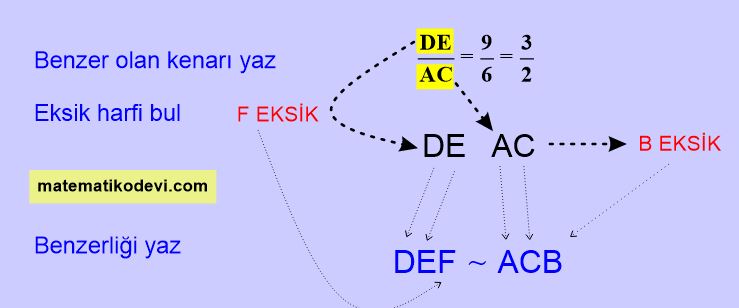
🤓 Kenar kenar kenar benzerliğinde orantılı kenarları gören açıların ölçüleri de eşittir.
2) Kenar – Açı – Kenar Benzerlik Şartı (KAK)
Bilgi: İki üçgen arasında birebir eşleme yapıldığında karşılıklı ikişer kenar uzunluklarının oranı ve bu iki kenar arasında kalan açılarının ölçüleri birbirine eşit ise bu iki üçgen benzer üçgenlerdir. Bu benzerliğe Kenar – Açı – Kenar (KAK) benzerlik şartı denir.
Örneğin;
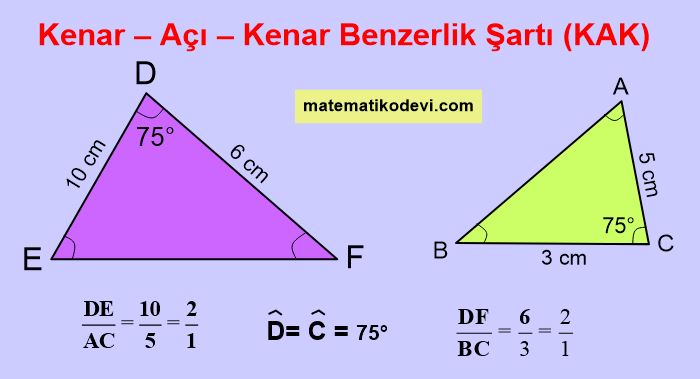
Yukarıda verilen iki üçgenin kenar uzunluklarını oranladığımızda iki kenarın oranlarının birbirine eşit ve oranları eşit olan kenarların arasında kalan açıların olduğunu görürüz. Bu durumda bu iki üçgen arasında Kenar-Açı-Kenar benzerliği vardır denir. Bu benzerliği yazarken sıraya dikkat ederek yazmalıyız.
🤓 Kenar – Açı – Kenar benzerliğini doğru sırayla yazmak için aşağıdaki yöntemi kullanabiliriz.

3) Açı – Açı Benzerlik Şartı (AA)
Bilgi: İki üçgen arasında birebir eşleme yapıldığında karşılıklı iki açılarının ölçüleri birbirine eşit ise bu iki üçgen birbirine benzer üçgenlerdir. Bu benzerliğe Açı – Açı (AA) benzerlik şartı denir.
Örneğin;
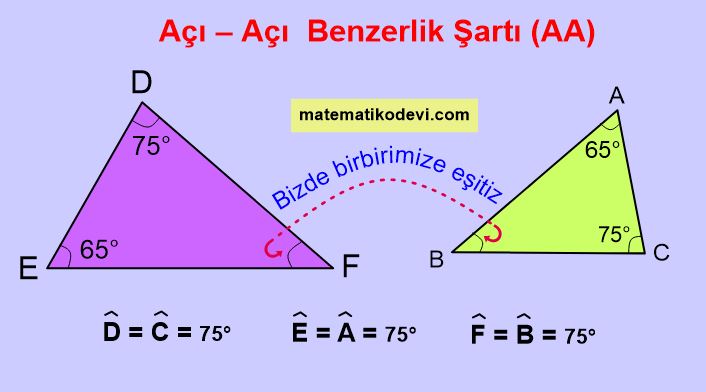
Yukarıda verilen iki üçgenin karşılıklı açıların ölçüleri birbirine eşit olduğunu görürüz. Bu durumda bu iki üçgen arasında Açı-Açı benzerliği vardır denir. Bu benzerliği yazarken sıraya dikkat ederek yazmalıyız.
🤓 Açı-Açı benzerliğini doğru sırayla yazmak için aşağıdaki yöntemi kullanabiliriz.
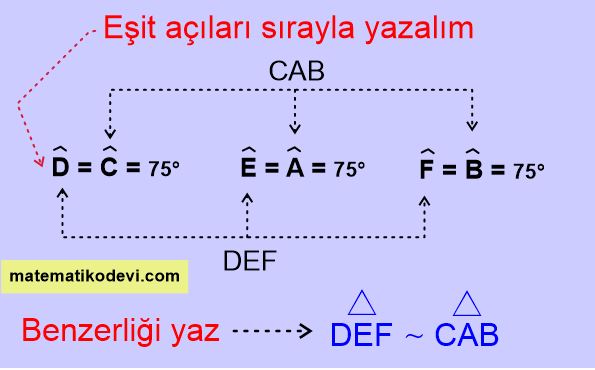
Not: İki üçgenin karşılıklı iki açısı eş ise üçüncü açısı da eştir. Bu yüzden bu benzerlik şartına Açı – Açı – Açı (AAA) benzerlik şartı da denilebilir.
EŞLİK VE BENZERLİK İLE İLGİLİ PRATİK BİLGİLER
🤓 Her eş üçgen aynı zamanda benzerdir, ancak her benzer üçgen aynı zamanda eş üçgen olmak zorunda değildir.
🤓 Benzer üçgenlerin benzerlik oranı 1 ise bu iki üçgen aynı zamanda eş üçgenlerdir.
🤓 İki üçgenin benzerlik oranı k ise çevrelerinin , kenarortaylarının ,açıortaylarının ve yüksekliklerinin oranı da kg’dır.
Örneğin iki üçgenin benzerlik oranı 3 ise bu iki üçgenin çevrelerinin , kenarortaylarının ,açıortaylarının ve yüksekliklerinin oranı da 3’dür.
🤓 İki üçgenin benzerlik oranı k ise alanları oranı da k2‘dir.
Örneğin iki üçgenin benzerlik oranı 3 ise bu iki üçgenin alanları oranı 9’dur.
Üçgenlerde Eşlik ve Benzerlik Test
Yeni Nesil Soru
🎥 Bir Soru Bir Video 🎥
Soru: KLM∼DEF ve |LM|=10 cm , |EF|=15 cm ve |KM|=6 cm olduğuna göre ;
- m( \widehat{MLK} ) = m( \widehat{FED} )
- |DE|= 9 cm
- KLM üçgeninin alanı 8 cm2 ise DEF üçgeninin alanı 9 cm2 ‘dir.
- KLM üçgeninin LM kenarına ait kenarortayı 14 cm ise DEF üçgeninin EF kenarına ait kenarortayı 21 cm’dir.
- |KL|= 12 cm
Yukarıda verilen ifadelerden kaç tanesi doğrudur?
| A) 5 | B) 4 | C) 3 | D) 2 |
Çözüm:

