Pisagor Bağıntısı Konu Anlatımı
Kazanım: Pisagor bağıntısını oluşturur; ilgili problemleri çözer.
Pisagor Bağıntısını Oluşturma ve İlgili Problemleri Çözme konu anlatımı aşağıda yapılmıştır.
Bu konuda neler öğreneceğiz :
Pisagor Bağıntısı
Bilgi: Bir dik üçgende 90 derecelik açının karşısındaki kenara hipotenüs denir.Hipotenüsün dışındaki diğer iki kenara dik kenar denir.

Bir dik üçgende ;
✅ Dik kenarların uzunluklarının karelerinin toplamı , hipotenüsün uzunluğunun karesine eşittir.
✅ Dik üçgenin kenar uzunlukları arasındaki bu ilişkiye Pisagor bağıntısı denir.
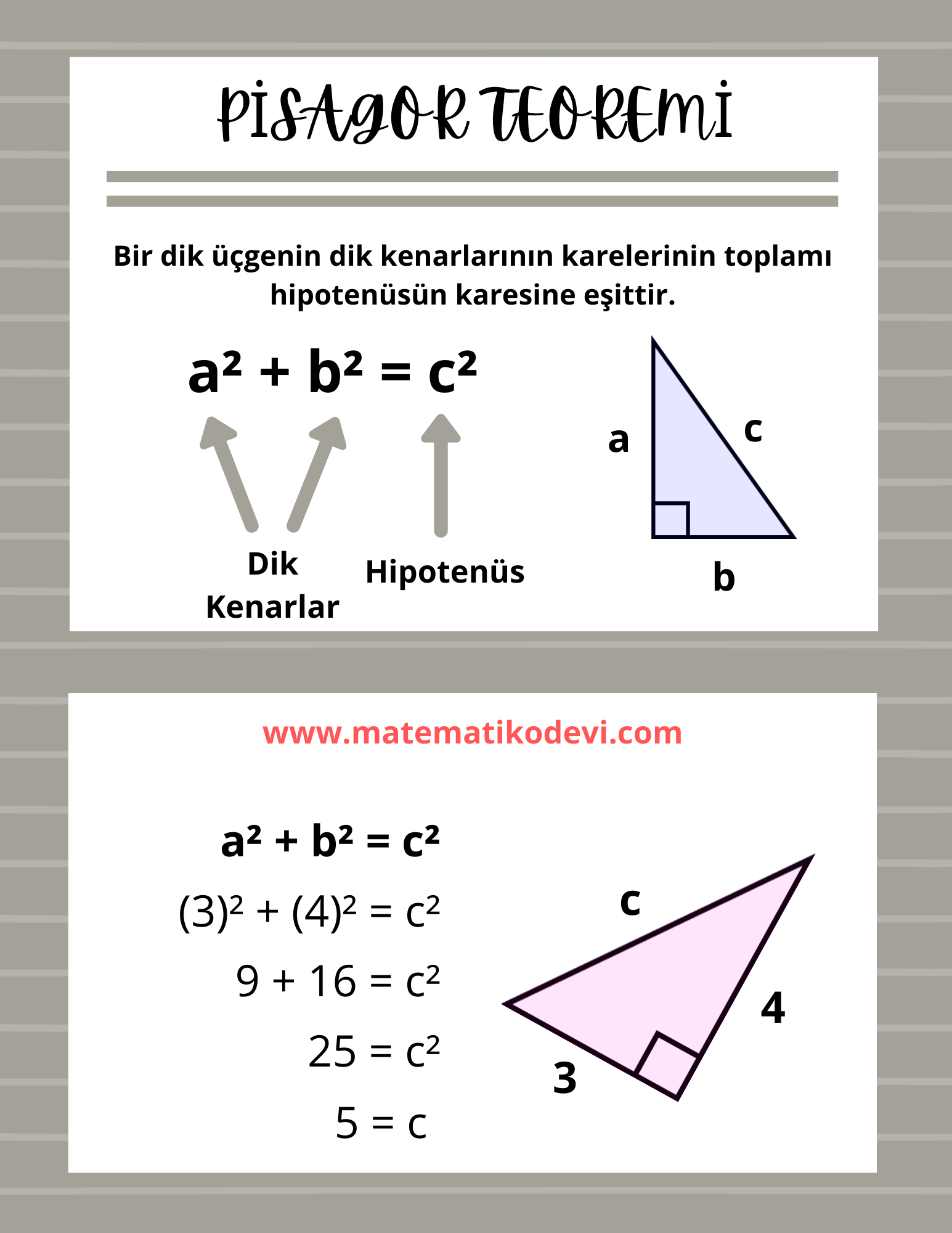
Aşağıda verilen görselde dik üçgene ait Pisagor bağıntısı verilmiştir.

Örnek:

Yukarıda verilen ABC dik üçgeninde hipotenüsün uzunluğunu bulunuz.
Çözüm:
✅ Dik kenarların karelerinin toplamı , hipotenüsün karesine eşittir.
➡️ 62 + 82 = x2
➡️ 36 + 64 = x2
➡️ 100 = x2 ( Hangi sayının karesi 100 yapar )
➡️ x = 10 cm
✅ 100 = x2 ifadesinde x’i bulurken her iki tarafın karekökünü alabiliriz.
➡️ \sqrt {x^2}=\sqrt {100}
➡️ x^2 karekök dışına x olarak çıkar. 100 karekök dışına 10 olarak çıkar.
➡️ x=10 cm
Örnek:

Yukarıda verilen ABC dik üçgeninde dik kenarın uzunluğunu bulunuz.
Çözüm:
✅ Dik kenarların karelerinin toplamı , hipotenüsün karesine eşittir.
➡️ 122 + x2 = 132
➡️ 144 + x2 = 169
➡️ x2 = 169 – 144
➡️ x2 = 25 ( Hangi sayının karesi 25 yapar )
➡️ x = 5 cm
✅ x2 = 25 ifadesinde x’i bulurken her iki tarafın karekökünü alabiliriz.
➡️ \sqrt {x^2}=\sqrt {25}
➡️ x^2 karekök dışına x olarak çıkar. 25 karekök dışına 5 olarak çıkar.
➡️ x = 5 cm
Örnek:

Yukarıda verilen ABC dik üçgeninde dik kenarın uzunluğunu bulunuz.
Çözüm:
✅ Dik kenarların karelerinin toplamı , hipotenüsün karesine eşittir.
➡️ 72 + x2 = 92
➡️ 49 + x2 = 81
➡️ x2 = 81 – 49
➡️ x2 = 32 ( Hangi sayının karesi 32 yapar ) ❓
➡️ Buradan x ‘i bulmamız zor olacağı için aşağıdaki yönteme göre x ‘i bulalım.
✅ x2 = 32 ifadesinde x’i bulurken her iki tarafın karekökünü alabiliriz.
➡️ \sqrt {x^2}=\sqrt {32}
➡️ x^2 karekök dışına x olarak çıkar.
➡️ 32 karekök dışına çıkmaz \sqrt {32} olarak kalır.
➡️ \sqrt {32} ifadesini 4\sqrt {2} ifadesine dönüştürürüz.
➡️ x = 4\sqrt {2} cm
KENAR UZUNLUKLARI TAM SAYI OLAN ÖZEL DİK ÜÇGENLER
Bazı dik üçgenler sorularda sıkça sorulmaktadır. Bu dik üçgenlerde Pisagor bağıntısını kullanarak istenen kenarı bulabiliriz. Ancak bu sıkça sorulan dik üçgenleri ezberleyerek Pisagor bağıntısı yapmadan hızlı bir şekilde bulabiliriz. Bu şekilde diğer sorulara zaman kazanmış oluruz. Şimdi bu sıkça sorulan üçgenleri inceleyelim.
(3-4-5) Dik Üçgeni:
Kenar uzunlukları (3 – 4 – 5) sayıları veya bu sayıların katı olan bütün üçgenler dik üçgendir.
(6 – 8 – 10), (9 – 12 – 15), … gibi.

(5-12-13) Dik Üçgeni:
Kenar uzunlukları (5 – 12 – 13) sayıları ve bu sayıların katı olan bütün üçgenler dik üçgenlerdir.
(10 – 24 – 26), (15 – 36 – 39),(20 – 48 – 52), … gibi.

(8-15-17) Dik Üçgeni:
Kenar uzunlukları (8 – 15 – 17) sayıları ve bu sayıların katı olan bütün üçgenler dik üçgenlerdir.
(16 – 30 – 34), (24 – 45 – 51),(32 – 60 – 68), … gibi.

(7-24-25) Dik Üçgeni:
Kenar uzunlukları (7– 24– 25) sayıları ve bu sayıların katı olan bütün üçgenler dik üçgenlerdir.
(14– 48– 50), (21– 72– 75),(28– 96– 100), … gibi.

Not: Birden fazla dik üçgenin olduğu sorularda kenar bilgisi en çok verilen dik üçgenden işlem yapmaya başlarız.
Örnek:

Yukarıdaki şekilde verilenlere göre |AE| kaç cm ‘dir?
✅ Kenar bilgisi en fazla verilen ABC üçgeninden başlamalıyız.
➡️ ABC üçgeninde pisagor bağıntısını uygulayalım.
➡️ 62 + 42 = |AC|2
➡️ 36 + 16 = |AC|2
➡️ 52 = |AC|2 ( iki tarafın karekökünü alırız.) 💡
➡️ \sqrt {52} = \sqrt {|AC|^2}
➡️ |AC|2 kök dışına |AC| olarak çıkar. \sqrt {52} ifadesi kök dışına çıkmaz.
➡️ |AC| = \sqrt {52} cm
✅ Şimdi pisagor bağıntısını ACD üçgenine uygulayalım.
➡️ \sqrt {52}2 + 32 = |AD|2 (\sqrt {52} ‘nin karesi 52 olur)💡
➡️ 52 + 9 = |AD|2
➡️ 61 = |AD|2
➡️ |AD| = \sqrt {61} cm
✅ Şimdi pisagor bağıntısını ADE üçgenine uygulayalım.
➡️ \sqrt {61}2 + \sqrt {3}2 = |AE|2
(\sqrt {61} ‘in karesi 61 olur.) 💡
(\sqrt {3} ‘ün karesi 3 olur.) 💡
➡️ 3 + 61 = |AE|2
➡️ 64 = |AE|2 ( hangi sayının karesi 64 olur.) 💡
➡️ |AE| = 8 cm
Kareli Bir Zemin Üzerinde Pisagor Bağıntısını Kullanarak İki Nokta Arasındaki Uzaklığı Hesaplama
Kareli zeminde iki nokta arasındaki uzaklığı pisagor bağıntısına göre hesaplayabilmek için noktalar aynı doğrultuda olmamalıdır. Noktalar aynı doğrultuda olursa pisagor bağıntısına gerek kalmaz. Direk yatay veya dikey uzunluğunu sayabiliriz.
Bilgi: Pisagor bağıntısını kullanarak iki nokta arasındaki uzaklığı hesaplamak için ;
✅ Verilen iki nokta birleştirilir.
✅ Birleştirdiğimiz bu doğru parçası hipotenüs olacak şekilde dik üçgen oluşturulur.
✅ Pisagor bağıntısını uygulayıp iki nokta arasındaki uzaklık hesaplanır.
Örnek:

Yukarıda kareli zeminde verilen A ve B noktalarının arasındaki uzaklığı hesaplayalım.
1.Adım: Verilen iki nokta birleştirilir.

2.Adım: Birleştirdiğimiz bu doğru parçası hipotenüs olacak şekilde dik üçgen oluşturulur.

3.Adım: Pisagor bağıntısını uygulayıp iki nokta arasındaki uzaklık hesaplanır

➡️ 32 + 62 = |AB|2
➡️ 9 + 36 = |AB|2
➡️ 45 = |AB|2 ( her iki tarafın karekökünü alalım )
➡️ \sqrt {45} = \sqrt {|AB|^2}
➡️ |AB| = \sqrt {45} br
➡️ |AB| = 3\sqrt {5} br
Not: Kenar uzunlukları verilen bir üçgenin dik üçgen olup olmadığını tespit etmek için ;
✅ En küçük iki kenarın kareleri toplamı , en büyük kenarın karesine eşit olmalıdır.
Örnek:
Aşağıda kenar uzunlukları verilen üçgenlerden hangisi veya hangileri dik üçgendir?
✅ |AB| = 9 cm , |BC| = 5 cm , |AC| = 10 cm
➡️ En küçük iki kenarın kareleri toplamı
52 + 92 =
25 + 81 =
106
➡️ En büyük kenarın karesi
102 =
100
➡️ En küçük iki kenarın kareleri toplamı ile En büyük kenarın karesi birbirine eşit değildir.
106 ≠ 100 ( Eşit olmadığı için ABC üçgeni dik üçgen değildir.)
✅ |DE| = 3 cm , |EF| = 3\sqrt {3} cm , |DF| = 6 cm
➡️ En küçük iki kenarın kareleri toplamı
32 + (3\sqrt {3})2 =
9 + 27 =
36
➡️ En büyük kenarın karesi
62 =
36
➡️ En küçük iki kenarın kareleri toplamı ile En büyük kenarın karesi birbirine eşittir.
36 = 36 ( Eşit olduğu için DEF üçgeni dik üçgendir.)
Not: Merdiven basamağı sorularında merdivenin yatay uzunlukları toplamı dik üçgenin dik kenarına ait yatay uzunluğu , merdivenin dikey uzunlukları toplamı dik üçgenin dik kenarına ait dikey uzunluğu oluşturur.


Pisagor Bağıntısı Test 1
Pisagor Bağıntısı Test 2
🎥 Bir Soru Bir Video 🎥
Soru:

Yukarıda 120 cm uzunluğunda olan Mustafa’nın saat 8:00 ‘ de gölgesi verilmiştir.Mustafa ve gölgesinin A ve B noktaları arasındaki en kısa mesafe 200 cm ‘dir.Gölgenin boyu güneşin hareketinden dolayı her 20 dakikada 10 cm kısalmaktadır.
Buna göre saat kaçta Mustafa ‘nın boyu ile gölgesi ( A noktası ile B noktası ) arasındaki en kısa mesafe 130 cm olur? ( A noktasının yeri güneşin hareketine göre değişmektedir. )
Çözüm:

