Doğrusal Denklemlerin Grafiğini Çizme Konu Anlatımı
Kazanım: Doğrusal denklemlerin grafiğini çizer.
Bu konuda neler öğreneceğiz :
Doğrusal Denklemlerin Grafiği
Bilgi: ax+by+c=0 biçimindeki denklemlere doğrusal denklem denir. Bu doğrusal denklemler koordinat sisteminde bir doğru oluşturur.
Aşağıda verilen görselde mavi çizgiler doğrusal denklemlerin koordinat sisteminde oluşturduğu doğrulara örnek olarak verilmiştir. Bu mavi çizgilere doğrusal denklem grafiği denir.
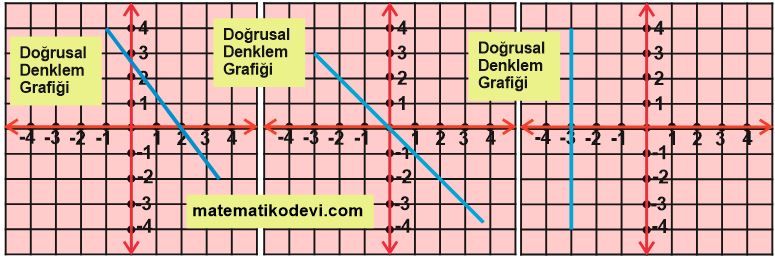
Şimdi bu doğrusal denklem grafiklerinin nasıl çizileceğini öğrenelim.
Doğrusal denklem grafiklerini 3 başlıkta eksenlere paralel olan doğru grafikleri , orijinden geçen doğru grafikleri ve eksenleri kesen doğru grafikleri olmak üzere 3 başlıkta ele alacağız ele alacağız.
1) Eksenlere Paralel Olan Doğru Grafiklerini Çizme
Koordinat sisteminde x ekseni ve y ekseni olmak üzere iki eksen olduğu için bu başlığı x eksenine paralel doğru grafiği ve y eksenine paralel doğru grafiği olmak üzere iki başlık olarak göreceğiz.
A) x eksenine paralel olan doğru grafiğini çizme :
Bilgi: Eğer bir denklemde sadece y değişkeni varsa bu denklemin grafiği x eksenine paraleldir.
✅ y=4 , y=-5 , 2y-6=0 …… gibi denklemler sadece y değişkeninden oluştuğu için x eksenine paraleldir.
✅ x eksenine paralel doğru grafiğini çizmek için denklemin y eksenine ait a noktası bulunup işaretlenir ve x eksenine paralel olacak şekilde düz bir doğru çizilir.
Şimdi x eksenine paralel olan doğru grafiğini çizmeyi aşağıdaki uygulamalı örneklerle pekiştirelim.
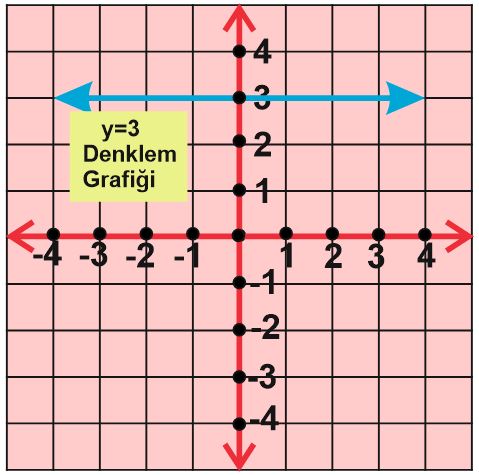
Örnek: y=3 denkleminin grafiğini koordinat sisteminde çizelim.
y=3 denkleminde y ‘nin değeri 3 olduğu için y =3 noktasını işaretleyip x eksenine paralel bir çizgi çizeriz.
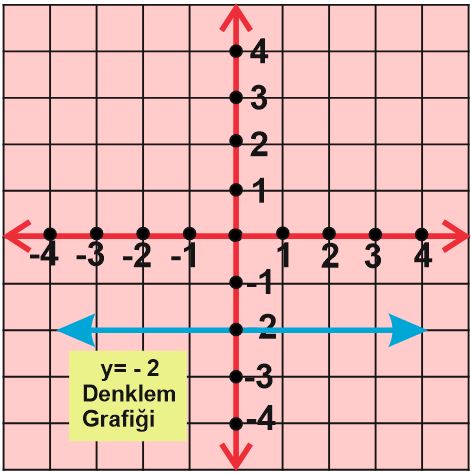
Örnek: y=-2 denkleminin grafiğini koordinat sisteminde çizelim.
y=-2 denkleminde y ‘nin değeri -2 olduğu için y =-2 noktasını işaretleyip x eksenine paralel bir çizgi çizeriz.
Örnek: 3y+12=0 denkleminin grafiğini koordinat sisteminde çizelim.
3y+12=0 denkleminde y ‘nin değerini bulmak için 3y+12=0 denklemini çözmeliyiz.
3y+12=0 🤓denklem çözme metodunu uygularız.
3y=-12
y = -4
3y+12=0 denkleminde y ‘nin değeri -4 olduğu için y =-4 noktasını işaretleyip x eksenine paralel bir çizgi çizeriz.
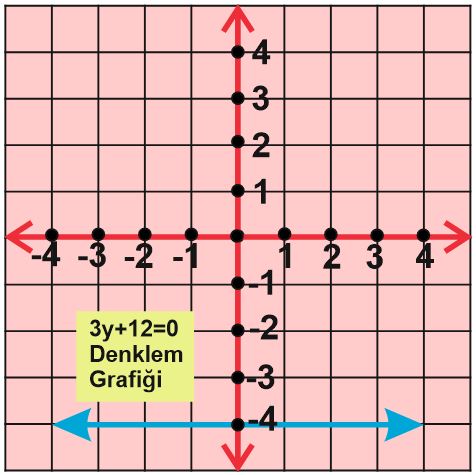
B) y eksenine paralel olan doğru grafiğini çizme :
Bilgi: Eğer bir denklemde sadece x değişkeni varsa bu denklemin grafiği y eksenine paraleldir.
✅ x=4 , x=-5 , 3x-9=0 …… gibi denklemler sadece x değişkeninden oluştuğu için y eksenine paraleldir.
✅ y eksenine paralel doğru grafiğini çizmek için denklemin x eksenine ait a noktası bulunup işaretlenir ve y eksenine paralel olacak şekilde düz bir doğru çizilir.
Şimdi y eksenine paralel olan doğru grafiğini çizmeyi aşağıdaki uygulamalı örneklerle pekiştirelim.
Örnek: x=2 denkleminin grafiğini koordinat sisteminde çizelim.
x=2 denkleminde x ‘in değeri 2 olduğu için x =2 noktasını işaretleyip y eksenine paralel bir çizgi çizeriz.
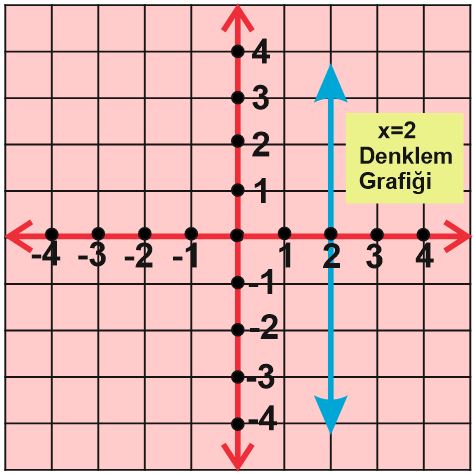
Örnek: x=-1 denkleminin grafiğini koordinat sisteminde çizelim.
x=-1 denkleminde x ‘in değeri -1 olduğu için x =-1 noktasını işaretleyip y eksenine paralel bir çizgi çizeriz.
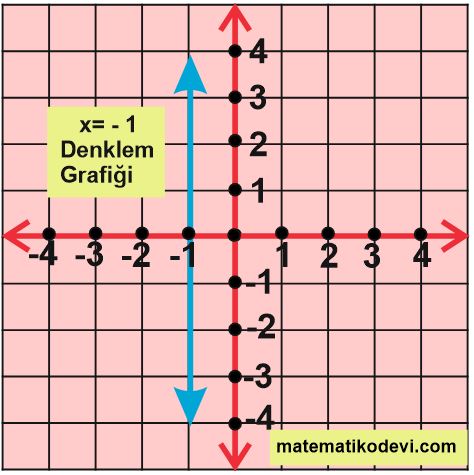
Örnek: 5x -20=0 denkleminin grafiğini koordinat sisteminde çizelim.
5x -20=0 denkleminde x ‘in değerini bulmak için 5x -20=0 denklemini çözmeliyiz.
5x -20=0 🤓denklem çözme metodunu uygularız.
5x=20
x = 4
5x -20=0 denkleminde x ‘in değeri 4 olduğu için x =4 noktasını işaretleyip y eksenine paralel bir çizgi çizeriz.
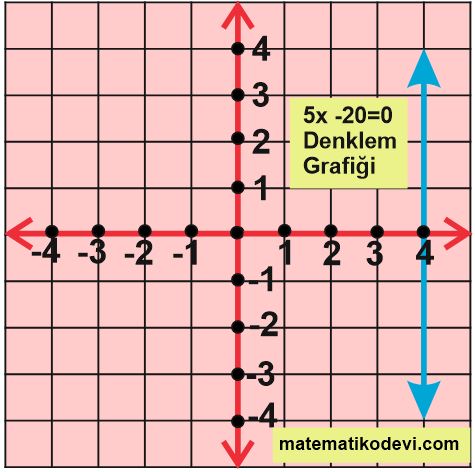
2) Orijinden Geçen Doğru Grafiklerini Çizme
Bilgi: x ve y değişkeni olan ve sabit terimi olmayan denklemlerin grafiği orijinden geçer.
✅ y=4x , y= -3x , 3x+5y=0 ….. gibi denklemler x ve y değişkeninden olup , sabit terimi olmadığı için bu denklemlerin grafikleri koordinat sisteminde orijinden geçer.
Orijinden geçen doğruları çizebilmek için orijin dışında bu doğru üzerinde olan nokta bulmamız lazım. Bu noktayı bulmak için değişkenlerden birine sıfırdan farklı bir değer verip diğer değişkenin değerini buluruz. Bulduğumuz noktayı koordinat ekseninde işaretleyip bu noktadan ve orijinden geçen bir doğru çizeriz. çizdiğimiz bu doğru denkleme ait doğrudur.
Şimdi orijinden geçen doğruların grafiğini çizmeyi aşağıdaki örneklerle pekiştirelim.
Örnek: y = 4x denkleminin grafiğini çizelim.
y = 4x denklemi sabit terimi olmadığı için orijinden (0,0) noktasından geçer.
👉 y = 4x denkleminin geçtiği ikinci bir nokta bulalım. Bu noktayı bulmak için değişkenlerden birine sıfırdan farklı bir değer vermeliyiz.
👉 y = 4x denkleminde x=1 değeri için y değerini bulalım.
y = 4·1=4
👉x=1 için y=4 oldu noktamız (1,4) olur.
👉 Şimdi (0,0) noktasından ve (1,4) noktasından geçen doğruyu çizelim. Çizdiğimiz bu doğru y=4x denklemine ait doğru grafiğidir.
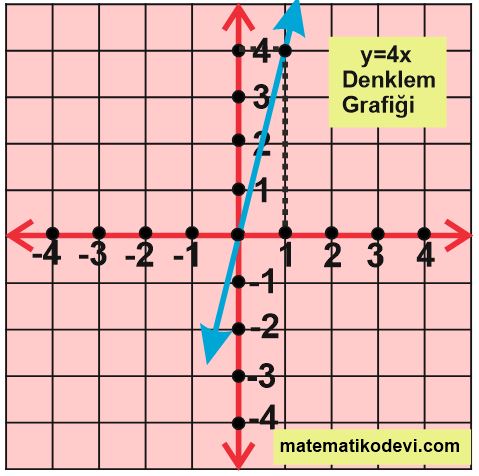
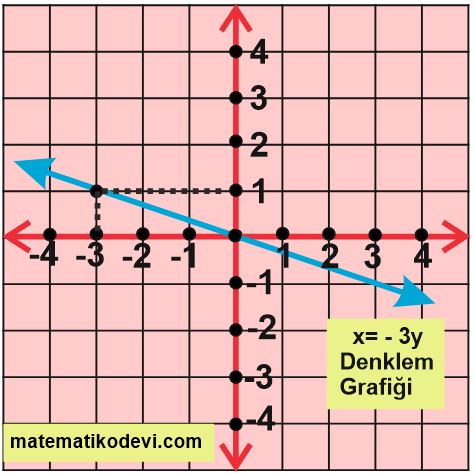
Örnek: x = -3y denkleminin grafiğini çizelim.
x = -3y denklemi sabit terimi olmadığı için orijinden (0,0) noktasından geçer.
👉 x = -3y denkleminin geçtiği ikinci bir nokta bulalım. Bu noktayı bulmak için değişkenlerden birine sıfırdan farklı bir değer vermeliyiz.
👉 x = -3y denkleminde y=1 değeri için x değerini bulalım.
x = (-3)·1=-3
👉y=1 için x=-3 oldu noktamız (-3,1) olur.
👉 Şimdi (0,0) noktasından ve (-3,1) noktasından geçen doğruyu çizelim. Çizdiğimiz bu doğru x = -3y denklemine ait doğru grafiğidir.
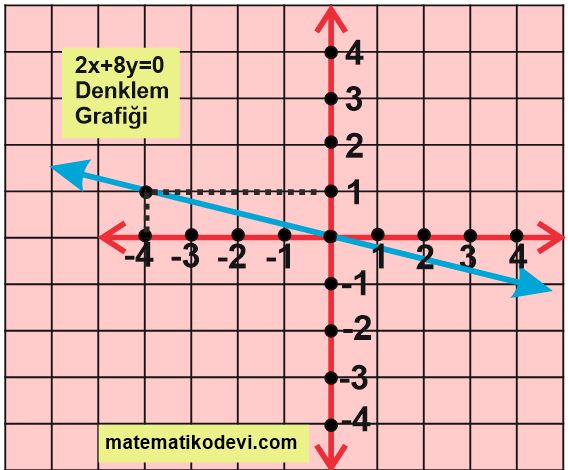
Örnek: 2x+8y=0 denkleminin grafiğini çizelim.
2x+8y=0 denklemi sabit terimi olmadığı için orijinden (0,0) noktasından geçer.
👉 2x+8y=0 denkleminin geçtiği ikinci bir nokta bulalım. Bu noktayı bulmak için değişkenlerden birine sıfırdan farklı bir değer vermeliyiz.
👉 2x+8y=0 denkleminde y=1 değeri için x değerini bulalım.
2x+8·1=0
2x+8=0
2x=-8
x=-4
👉 y=1 için x= -4 oldu noktamız (-4,1) olur.
👉 Şimdi (0,0) noktasından ve (-4,1) noktasından geçen doğruyu çizelim. Çizdiğimiz bu doğru 2x+8y=0 denklemine ait doğru grafiğidir.
3) Eksenleri Kesen Doğru Grafiğini Çizme:
Bilgi: x ve y değişkeni ile sabit terimden oluşan denklemlerin grafikleri koordinat sisteminde x ve y eksenini keser.
✅ 3x+5y-15=0 , 2x + 5y +10=0 , 4x+7y -28=0 ….. şeklindeki denklemler x ve y değişkeni ile sabit terimden oluştuğu için bu denklemlerin grafikleri koordinat sisteminde x ve y eksenini keser.
Eksenleri kesen denklemlerin grafiğini çizmek için;
👉 x değişkenine 0 değeri verip y değerini buluruz.
👉 y değişkenine 0 değeri verip x değerini buluruz.
👉 Oluşan iki nokta koordinat sisteminde işaretlenir.
👉 Bu iki noktadan geçen doğru çizilir.
Şimdi bu adımları uygulayıp eksenleri kesen denklemlerin grafiğini aşağıdaki örneklerle pekiştirelim.
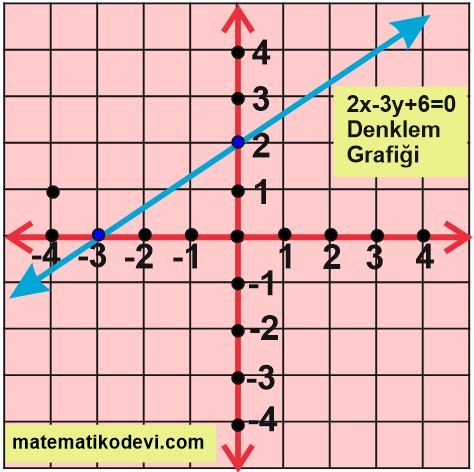
Örnek: 2x-3y+6=0 denkleminin grafiğini çizelim.
x ve y değişkeni ile sabit terimden oluştuğu için 2x-3y+6=0 denklemi koordinat sisteminde eksenleri keser.
👉 x değişkenine 0 değeri verip y değerini buluruz.
2·0-3y+6=0
-3y+6=0
-3y=-6
y=2
👉 y değişkenine 0 değeri verip x değerini buluruz.
2x-3·0+6=0
2x+6=0
2x=-6
x=-3
👉 Oluşan iki nokta koordinat sisteminde işaretlenir.
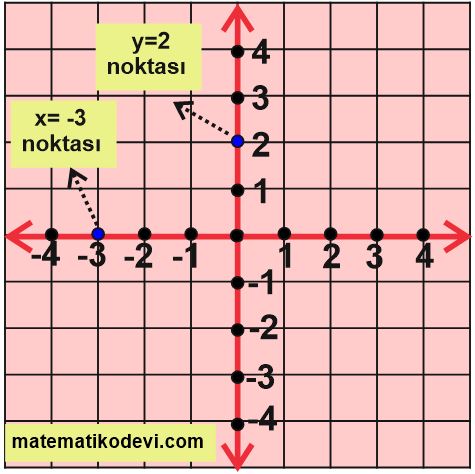
👉 Bu iki noktadan geçen doğru çizilir.
Yeni Nesil Soru
🎥 Bir Soru Bir Video 🎥
Soru: Halil aşağıdaki görseldeki gibi bir oyun tasarlıyor. Bu oyunda giriş ekranına bir sayı yazılıyor ve bu sayı sonuç ekranında başka bir sayıya dönüşüyor.
Giriş ekranına yazılan sayı aşağıdaki adımlardan geçerek sonuç ekranındaki sayıya dönüşmektedir.
- Giriş ekranına yazılan sayıdan 6 çıkar
- Çıkan sonucu 4 ile çarp
- çıkan sonuca 12 ekle
- Çıkan sonucu 3 ile böl
- Bulduğumuz sayıyı sonuç ekranına yaz
Halil yukarıdaki oyunda giriş ekranındaki sayıyı x ekseni , sonuç ekranındaki sayıyı y ekseni olacak şekilde oluşan sıralı ikilileri koordinat siteminde nokta olarak işaretleyip sonra bu noktaları birleştiriyor.
Buna göre Halil’in birleştirdiği noktaların görüntüsü aşağıdakilerden hangisi gibi olabilir?
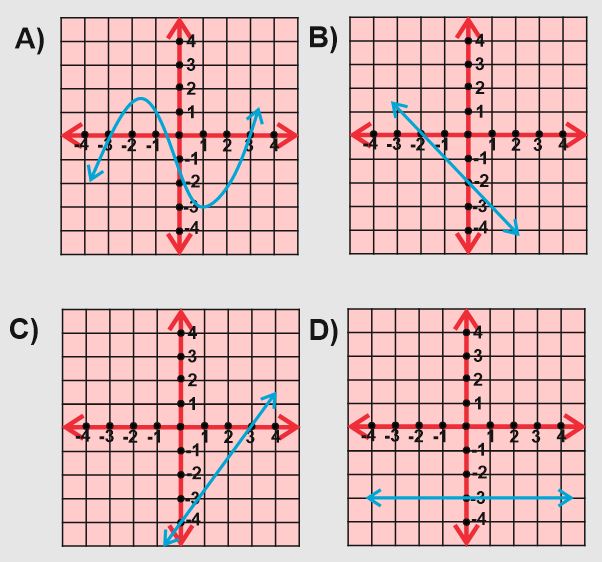
Çözüm:
Konu Anlatımın Devamı : https://www.matematikodevi.com/dogrusal-iliski-iceren-gercek-hayat-durumlari/

