Dağılma Özelliği ve Ortak Çarpan Parantezine Alma Konu Anlatımı – 6.Sınıf

Dağılma Özelliği ve Ortak Çarpan Parantezine Alma 6.Sınıf 1.dönem konularındandır.

Kazanım: Doğal sayılarda ortak çarpan parantezine alma ve dağılma özelliğini uygulamaya yönelik işlemler yapar.

DAĞILMA ÖZELLİĞİ

Çarpma işleminin dağılma özelliğini kullanmak bazı işlemlerde kolay çarpma yapmamızı sağlar.

Örneğin 1004·21 sayısını direk çarpmak yerine 1004 sayısını 1000 ve 4 şeklinde ayırıp 21’i 1000 ve 4 ile çarpıp çıkan sonuçları toplarız.

👉 1004·21

👉 (1000+4)·21

👉 1000·21+4·21

👉 21000+84

👉 21084

Yukarıdaki örnekteki gibi dağılma özelliği bazı çarpma işlemlerinde sonucu kolay bulmamızı sağlar.

Dağılma özelliği çarpmanın toplama üzerine dağılma özelliği ve çarpmanın çıkarma üzerine dağılma özelliği üzerine olmak üzere iki başlığa ayrılır. Şimdi bu başlıkları aşağıda detaylı olarak inceleyelim.

ÇARPMANIN TOPLAMA ÜZERİNE DAĞILMA ÖZELLİĞİ

Bilgi: Bir doğal sayıyı parantez içinde toplam biçimindeki doğal sayılarla çarparken, bu doğal sayı ile toplam biçimindeki doğal sayılar ile ayrı ayrı çarpılır ve bu çarpımlar toplanır. Yapılan bu işleme çarpma işleminin toplama işlemi üzerine dağılma özelliği denir.

Örneğin 7 x ( 11 + 5 ) ifadesinde parantez içinde toplam biçimindeki doğal sayılarla çarpma işlemini aşağıdaki gibi parantez içindeki sayılarla tek tek çarpıp toplarız.

7×( 11 + 5 )= 7×11 + 7×5

Yaptığımız bu işleme çarpmanın toplama işlemi üzerinde dağılma özelliği denir.

Örnek: 8×( 15 + 4 ) işlemini dağılma özelliği kullanarak yapalım.

Çözüm:

🤓Çarpım durumundaki 8’i önce 15 ile sonra 4 ile çarparız ve daha sonra bu sonuçları toplarız.

8×( 15 + 4 ) = ( 8×15 ) + ( 8× 4 ) = 120 + 32 = 152

Örnek: 13 x 102 işlemini dağılma özelliği kullanarak yapalım.

Çözüm:

🤓 Dağılma özelliğini yapabilmemiz için parantez içinde toplam durumunda sayı olması lazım. Bu nedenle 102 sayısını (100+2) şeklinde yazalım.

13×102 = 13×(100+2) ➡️ şimdi bu işeme dağılma özelliğini uygulayalım.

( 13×100 ) + ( 13× 2 )

1300+26

1326 olarak bulunur.

😯 Bu örnekte dağılma özelliğinin işlemlerde kolaylık sağladığını daha rahat görebilirsiniz.

ÇARPMANIN ÇIKARMA ÜZERİNE DAĞILMA ÖZELLİĞİ

Bilgi: Bir doğal sayıyı parantez içinde farkı alınan doğal sayılarla çarparken, bu doğal sayı ile farkı alınan doğal sayılar ile ayrı ayrı çarpılır ve bu çarpımlar çıkarılır. Yapılan bu işleme çarpma işleminin çıkarma işlemi üzerine dağılma özelliği denir.

Örneğin 9 x ( 21 – 7 ) ifadesinde parantez içinde farkı alınan doğal sayılarla çarpma işlemini aşağıdaki gibi parantez içindeki sayılarla tek tek çarpıp çıkarırız.

9×( 21 – 7 )= 9×21 – 9×7

Yaptığımız bu işleme çarpmanın çıkarma işlemi üzerinde dağılma özelliği denir.

Örnek: 16×( 30 – 5 ) işlemini dağılma özelliği kullanarak yapalım.

Çözüm:

Çarpım durumundaki 16’yı önce 30 ile sonra 5 ile çarparız ve daha sonra bu sonuçları birbirinden çıkartırız.

16 × ( 30 – 5 ) = ( 16 × 30 ) – ( 16 × 5 ) = 480 – 80= 400

Örnek: 8 × 97 işlemini dağılma özelliği kullanarak yapalım.

Çözüm:

🤓 Dağılma özelliğini yapabilmemiz için parantez içinde iki doğal sayının farkı durumunda sayı olması lazım. Bu nedenle 97 sayısını (100 – 3) şeklinde yazalım.

8 × 97 = 8×(100 – 3) ➡️ şimdi bu işeme dağılma özelliğini uygulayalım.

( 8×100 ) – ( 8× 3 )

800 – 24

776 olarak bulunur.

😯 Bu örnekte dağılma özelliğinin işlemlerde kolaylık sağladığını daha rahat görebilirsiniz.

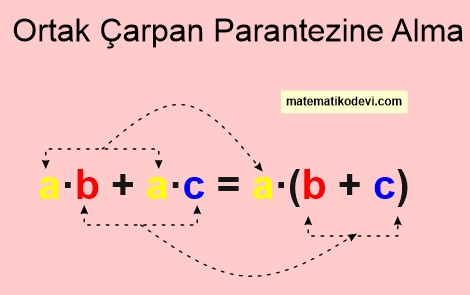
ORTAK ÇARPAN PARANTEZİNE ALMA

Bilgi: İki doğal sayının aynı doğal sayı ile ayrı ayrı çarpımlarının toplamı veya farkı bu iki doğal sayının toplamının veya farkının ortak olan doğal sayı ile çarpımına eşittir. Bu özelliğe ortak çarpan parantezine alma denir.

Örneğin 9×13 – 9×11 işlemini 9 ile 13’ü çarpıp sonra 9 ile 11’i çarptıktan sonra çıkan sonuçları birbirinden çıkararak yapabiliriz.

Yada aşağıdaki gibi ortak çarpan olan 9’u parantez dışına kalan sayıları parantez içine yazıp önce parantez içini yapabiliriz.

9×13 – 9×11 ➡️ 9 parantezine al

9×(13-11) ➡️parantez içini yapalım

9×2

18

Yaptığımız bu işleme ortak çarpan parantezine alma denir.

Örnek: 15 x 17 + 15 x 3 işlemini ortak çarpan parantezine alarak yapalım.

🤓 Ortak çarpan parantezine almadan yapacak olsaydık 15 ile 17’yi çarpacaktık, daha sonra 15 ile 3’ü çarpıp bu sonuçları toplayacaktık.

15 x 17 = 255

15 x 3 = 45

255 + 45 = 300

🤓 Ortak çarpan parantezine alarak yapacak olursak

15 x 17 + 15 x 3

15 x (17+3)

15 x(20)

300

😯 Yukarıdaki işlemleri incelediğimizde verilen işlemi ortak çarpan parantezine göre yapmak daha kolaydır.

Ortak Çarpan Parantezine Alma Yöntemini Kullanarak Dikdörtgenin Alanını Bulma

Ortak bir kenarı olan dikdörtgenlerden oluşan şeklin tamamının alanı sorulduğunda ortak çarpan parantezine alma yöntemi kullanılır.

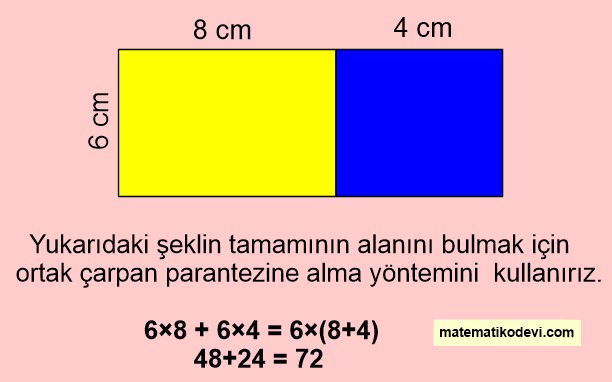
Yukarıdaki görselde verilen şeklin tamamının alanını bulmak için 2 yöntem kullanabiliriz.

1.Yöntem: 8 ile 6’yı çarpıp 4 ile 6’yı çarpıp çarpımları toplarız. (sarı ve mavi bölgelerin alanlarını bulup toplarız.)

Şeklin tamamının alanı ➡️ 6×8 + 6×4

2.Yöntem: 8 ile 4’ü toplayıp 6 ile çarparız. (sarı ve mavi bölgenin birleşiminin alanını hesaplarız.)

Şeklin tamamının alanı ➡️ 6×(8+4)

😯 O zaman 6×8 + 6×4 = 6×(8+4)

Dağılma Özelliğini Kullanarak Dikdörtgenin Alanını Bulma

Ortak bir kenarı olan dikdörtgenlerden oluşan şekilde dikdörtgenlerden birinin alanı sorulduğunda dağılma özelliğinden yararlanırız

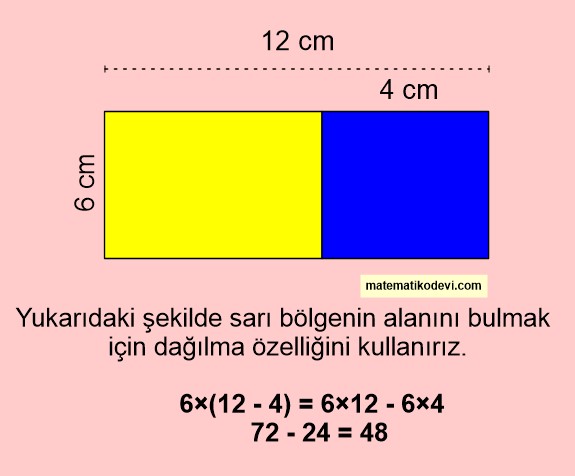
Not: Şeklin tamamının alanı sorulduğunda ortak çarpan parantezine alma yöntemi kullanılır. Şekli oluşturan parçalardan biri sorulduğunda dağılma özelliği kullanılır.

Dağıma Özelliği ve Ortak Çarpan Parantezine Alma Test ve Etkinlik

Dağılma özelliği ve ortak çarpan parantezine alma konusu ile ilgili test ve etkinlikleri aşağıdan çözebilirsiniz. İnternet hızından kaynaklı test ve etkinlikler açılmamış olursa sayfayı yenileyiniz.

Instagram adresimiz : https://www.instagram.com/matara_33/

🔻 Diğer konulara hızlı geçiş 🚀

⏪ Önceki Konu	Sonraki Konu ⏩
İşlem Önceliği Konu Anlatımı	Doğal Sayılarla Dört İşlem Yapmayı Gerektiren Problemler