Çokgenlerde Benzerlik Konu Anlatımı
Kazanım: Benzer çokgenlerin benzerlik oranını belirler, bir çokgene eş ve benzer çokgenler oluşturur.
Çokgenlerde Benzerlik Konu Anlatımı aşağıda detaylı bir şekilde anlatılmıştır. Konuya öğrendikten sonra en altta yer alan yeni nesil sorumuzu çözmeyi unutmayınız.
Bu konuda neler öğreneceğiz :
Benzer Çokgenler
Bilgi: İki çokgenin karşılıklı açılarının ölçüleri eşit ve karşılıklı kenar uzunlukları orantılı ise bu iki çokgene benzer çokgen denir.
Benzer çokgenlerde ;
✅ Karşılıklı açı ölçüleri eşit olmalıdır.
✅ Karşılıklı kenar uzunlukları orantılı olmalıdır.
Örnek:
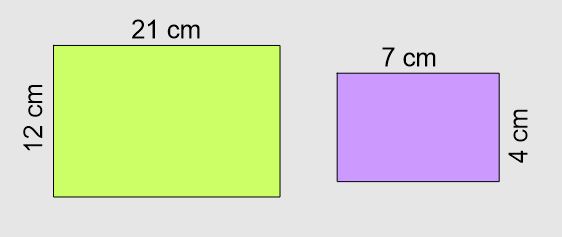
Yukarıda verilen iki çokgen benzer olup olmadığını inceleyelim.
👉 Karşılıklı açı ölçüleri eşit olmalıdır.
İki dikdörtgenin iç açıları 90° olduğu için karşılıklı açıları eşittir.
👉 Karşılıklı kenar uzunlukları orantılı olmalıdır.
Kısa kenarları oranı \dfrac{12}{4} = \dfrac{3}{1} = 3
Uzun kenarları oranı \dfrac{21}{7} = \dfrac{3}{1} = 3
🤓 Karşılıklı açıları eşit ve kenar uzunlukları orantılı olduğu için bu iki çokgen benzerdir.
Örnek:
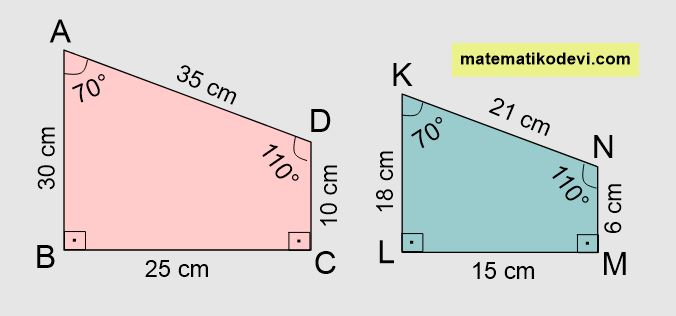
Yukarıda verilen iki çokgen benzer olup olmadığını inceleyelim.
👉 Karşılıklı açı ölçüleri eşit olmalıdır.
\widehat{A} = \widehat{K} = 70°
\widehat{D} = \widehat{N} = 110°
\widehat{C} = \widehat{M} = 90°
\widehat{B} = \widehat{L} = 90°
👉 Karşılıklı kenar uzunlukları orantılı olmalıdır.
\dfrac{|AB|}{|KL|} = \dfrac{30}{18} = \dfrac{5}{3}
\dfrac{|AD|}{|KN|} = \dfrac{35}{21} = \dfrac{5}{3}
\dfrac{|DC|}{|NM|} = \dfrac{10}{6} = \dfrac{5}{3}
\dfrac{|BC|}{|LM|} = \dfrac{25}{15} = \dfrac{5}{3}
🤓 Karşılıklı açıları eşit ve kenar uzunlukları orantılı olduğu için bu iki çokgen benzerdir.
🤓 Bu benzerliği sıraya göre yazmalıyız. ADCB∼KNML
Üçgende Benzerlik Teoremleri
Üçgende benzerlik teoremleri , benzerlik sorularını daha hızlı şekilde çözmemizi sağlayan yöntemlerdir. Bu yöntemleri açı – açı – açı benzerlik teoreminin pratik hali olarak düşünebiliriz .Sorularda aşağıdaki şekillerden birini gördüğümüzde o şeklin verilen formülünü uygulayarak soruları daha hızlı çözeriz.
Thales Teoremi
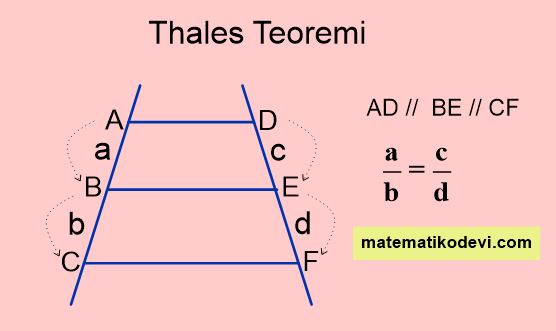
Temel Benzerlik Teoremi
Bilgi: Bir üçgenin bir kenarına paralel olan ve diğer iki kenarını kesen bir doğru, kestiği kenarları orantılı parçalara ayırır. Bu teoreme temel orantı teoremi denir.
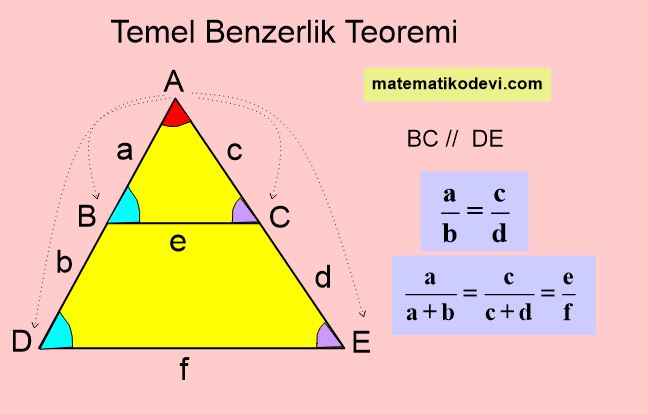
Yukarıdaki görselde ABC ve ADE üçgenlerinin açılarını karşılaştırdığımızda aynı renkteki açıların ölçüleri paralellikten dolayı eşittir. Bu durumda ABC ve ADE üçgenleri arasında açı-açı benzerliği vardır. Her zaman bu tarz sorularda açı-açı benzerliğini aramak yerine yukarıdaki temel benzerlik teoremini kullanırız.
Kelebek Benzerliği
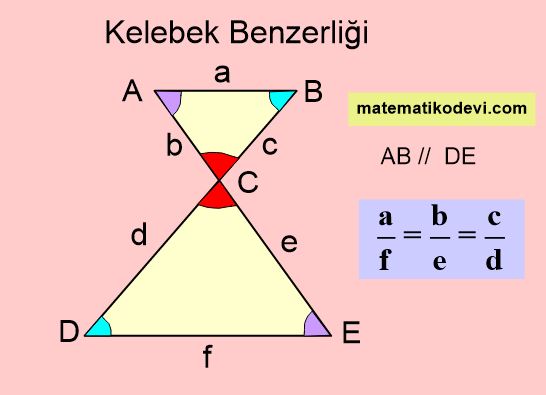
Yukarıdaki görselde ABC ve EDC üçgenlerinin açılarını karşılaştırdığımızda aynı renkteki açıların ölçüleri paralellikten dolayı eşittir. Bu durumda ABC ve EDC üçgenleri arasında açı-açı benzerliği vardır. Her zaman bu tarz sorularda açı-açı benzerliğini aramak yerine yukarıdaki kelebek benzerliğini kullanırız.
Dik Üçgen Benzerliği
Dik üçgenlerin birer köşesinden dik olarak kesişmesi ile oluşan modellerde dik üçgen benzerliği vardır.

Yukarıda verilen görseli incelediğimizde iki üçgen C noktasından dik olarak kesişmişlerdir. Bu durumda bu iki üçgende açı-açı benzerliğini kullanarak kenarları oranlayabiliriz.
Benzerlik Hap Bilgi :

Yeni Nesil Soru
🎥 Bir Soru Bir Video 🎥
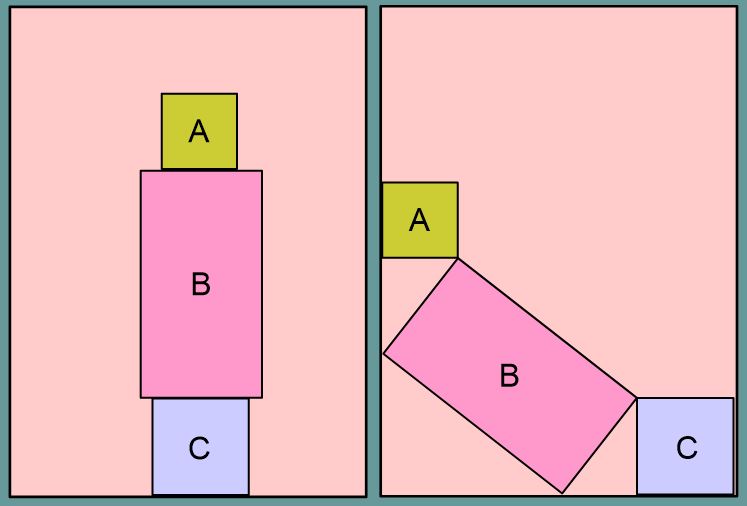
Mira dikdörtgen bir zeminin içine kare şeklindeki A ve C kutuları ile dikdörtgen şeklindeki B kutusunu görseldeki gibi üst üste koyduğunda ( { \sqrt {180} } +6) cm yüksekliğine ulaşıyor. Daha sonra bu kutular devrilip ikinci görseldeki gibi duruyor.
- Dikdörtgenin uzun kenarı , kısa kenarının 3 katıdır.
- C karesinin alanı , A karesinin alanının 4 katıdır.
Buna göre B kutusunun görünen yüzünün alanı kaç cm2 ‘dir?
| A) 50 | B) 60 | C) 70 | D) 80 |
Çözüm:

