Cebirsel İfadeler Konu Anlatımı
Kazanım: Sözel olarak verilen bir duruma uygun cebirsel ifade ve verilen bir cebirsel ifadeye uygun sözel bir durum yazar.
Bu konuda neler öğreneceğiz :
CEBİRSEL İFADELER
Bilgi: İçerisinde en az bir bilinmeyen bulunan ifadelere cebirsel ifade denir. Değişkenler genellikle a,b,x,y,…. gibi küçük harfler kullanılarak gösterilir.
✅ Bir ifadenin cebirsel ifade olabilmesi için en az bir bilinmeyenden oluşması lazım.
➡️ Miray’ın yaşı 15’dir. Miray’ın yaşının 4 katı ifadesi cebirsel ifade olmaz. Çünkü bilinmeyen bir ifade bulunmamaktadır.(Miray’ın yaşı biliniyor.)
➡️ Yağmur’un yaşının 4 katı ifadesi cebirsel ifade olur. Çünkü bilinmeyen ifade vardır. (Yağmur’un yaşı bilinmiyor.)
✅ Cebirsel ifadelerde bilinmeyen ifadeye değişken denir. Değişken harf yada sembol kullanılarak gösterilir.
Örnek: Kaan’ın yaşının 4 katı ifadesini cebirsel ifade olarak yazalım.
➡️ Kaan’ın yaşını bilmediğimiz için a diyelim.
➡️ Kaan’ın yaşının 4 katını 4×a olarak gösteririz.
➡️ Bu ifadeyi zamanla 4a şeklinde yazıp aradaki çarpma işaretini belirtmeyiz.

Örnek: Bir sayının 5 katının 3 eksiği ifadesini cebirsel ifade olarak yazalım.
➡️ Sayıyı bilmediğimiz için x diyelim.
➡️ Sayının 5 katını 5·x olarak gösteririz.
➡️ Sayının 5 katının 3 eksiğini 5·x – 3 olarak gösteririz.
➡️ Bu ifadeyi zamanla 5x-3 şeklinde yazıp aradaki çarpma işaretini belirtmeyiz.
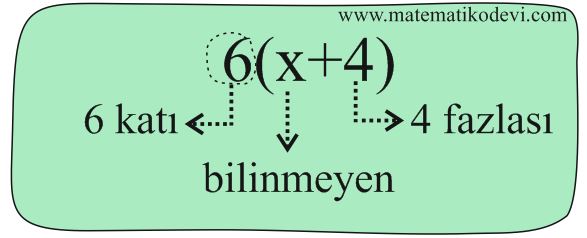
Örnek: 6(x+4) cebirsel ifadesini sözel olarak ifade edelim.
➡️ Bilinmeyen(değişken) sayı x’dir.
➡️ Bilinmeyen(değişken) sayıya 4 eklemiş.
➡️ Bilinmeyen(değişken) sayıya 4 ekledikten sonra 6 ile çarpmış.
6(x+4) ifadesi 👉 Bir sayının 4 fazlasının 6 katı demektir.
Örnek: Aşağıda verilen sözel ifade cebirsel ifade olarak ifade edilmiştir. Bu adımları inceleyelim.
✅ Bir sayının yarısının 5 eksiği ❓
➡️ Bilinmeyen sayı x olsun.
➡️ Bir sayının yarısı x’in yarısı 👉 \dfrac{x}{2}
➡️ Bir sayının yarısının 5 eksiği 👉 x’in yarısının 5 eksiği = \dfrac{x}{2} -5
✅ Bir sayının 5 eksiğinin yarısı ❓
➡️ Bilinmeyen sayı x olsun.
➡️ Bir sayının 5 eksiği👉 x’in 5 eksiği = x-5
➡️ Bir sayının 5 eksiğinin yarısı 👉 x’in 5 eksiğinin yarısı 👉 \dfrac{x-5}{2}
✅ Bir sayının 6 katının 8 fazlası ❓
➡️ Bilinmeyen sayı a olsun
➡️ Bir sayının 6 katı ( a’nın 6 katı) = 6a
➡️ Bir sayının 6 katının 8 fazlası ( a’nın 6 katının 8 fazlası) = 6a+8
✅ Bir sayının 8 fazlasının 6 katı ❓
➡️ Bilinmeyen sayı a olsun.
➡️ Bir sayının 8 fazlası ( a’nın 8 fazlası) = a+8
➡️ Bir sayının 8 fazlasının 6 katı ( a’nın 8 fazlasının 6 katı) = (a+8)×6
➡️ (a+8)×6 ifadesini 6(a+8) şeklinde yazarız.
Örnek: 5(x+11) cebirsel ifadesini sözel olarak ifade edelim.
✅ Cebirsel ifadeyi sözel olarak ifade ederken işlem önceliği basamaklarına uyarız.
✅ Önce parantez içinden başlarız.
➡️ Bir sayının 11 fazlası = (x+11)
➡️ Bir sayının 11 fazlasının 5 katı = 5 (x+11)
🤓 Aşağıda verilen cebirsel ifadeleri sözel olarak ifade ettikten sonra verilen sözel ifadelerle karşılaştırıp cevaplarınızı kontrol ediniz.

Terim Nedir ?
Bilgi: Cebirsel ifadede ”+” veya ”-” işaretleri ile birbirinden ayrılan her bir ifadeye terim denir.
Cebirsel ifadede terimleri bulmak için;
✅ ”+” veya ”-” işaretlerinin soluna ”/” işareti koyalım.
✅ Sonra arada kalan her bir ifadeyi terim olarak yazarız.
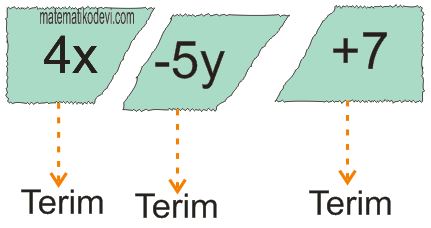
Örnek: 4x-5y+7 cebirsel ifadesinin terimlerini bulalım.
➡️ 4x-5y+7 Cebirsel ifadesinde ”+” veya ”-” işaretlerinin soluna ”/” işareti koyalım.
➡️ 4x /-5y /+7
➡️ Terimleri 4x , -5y ve +7 ‘dir.
Sabit Terim Nedir ?
Bilgi: Cebirsel ifadede değişken içermeyen terime sabit terim denir.
Örnek: 8a-11 cebirsel ifadesinin sabit terimini bulalım.
➡️ 8a-11 Cebirsel ifadesinde değişkeni olmayan terim ”-11”
➡️ Sabit terim -11’dir.
Örnek: 6a-9b-14 cebirsel ifadesinin sabit terimini bulalım.
➡️ 6a-9b-14 Cebirsel ifadesinde değişkeni olmayan terim ”-14”
➡️ Sabit terim -14’dür.
Katsayı Nedir ?
Bilgi: Cebirsel ifadede değişkenlerle çarpım durumunda olan sayıya katsayı denir.
✅ Sabit terim bir katsayıdır.
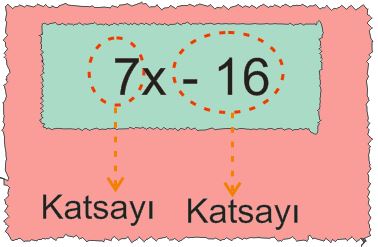
Örnek: 7x-16 cebirsel ifadesinin katsayılarını bulalım.
➡️ 7x-16 cebirsel ifadesinde değişken ile çarpım durumunda olan sayı 7’dir.
➡️ 7 bir katsayıdır.
➡️ Sabit terimi -16 olduğu için -16 bir katsayıdır.
➡️ 7x-16 cebirsel ifadesinin katsayıları 7 ve -16’dır.
Örnek: 5m-x+17 cebirsel ifadesinin katsayılarını bulalım.
➡️ 5m-x+17 cebirsel ifadesinde değişken ile çarpım durumunda olan sayılar 5 ve -1’dir.
➡️ 5 ve -1 katsayıdır.
➡️ Sabit terimi 17 olduğu için 17 bir katsayıdır.
➡️ 5m-x+17 cebirsel ifadesinin katsayıları 5,-1 ve 17’dir.

Benzer Terim Nedir ?
Bilgi: Cebirsel ifadede değişkenleri aynı olan terimlere benzer terim denir. Benzer terim olabilmesi için değişkenlerin üslerinin de aynı olması lazım.
Örnek: 7x-14b+9x+4b cebirsel ifadesinde benzer terimleri bulalım.
✅ Değişkeni x olan terimler
➡️ 7x ve 9x benzer terimlerdir.
✅ Değişkeni b olan terimler
➡️ -14b ve 4b benzer terimlerdir.
Cebirsel İfade Özet:


