Birinci Dereceden Bir Bilinmeyenli Denklemleri Çözme Konu Anlatımı
Kazanım: Birinci dereceden bir bilinmeyenli denklemleri çözer.
Bu konuda neler öğreneceğiz :
BİRİNCİ DERECEDEN BİR BİLİNMEYENLİ DENKLEMLER
Bilgi: a,b ∈ R ve a ≠ 0 olmak üzere ax + b = 0 şeklinde ifade edilebilen denklemlere birinci dereceden bir bilinmeyenli denklemler denir. Bu denklemde a ve b katsayı , x ise bilinmeyendir.(değişken)
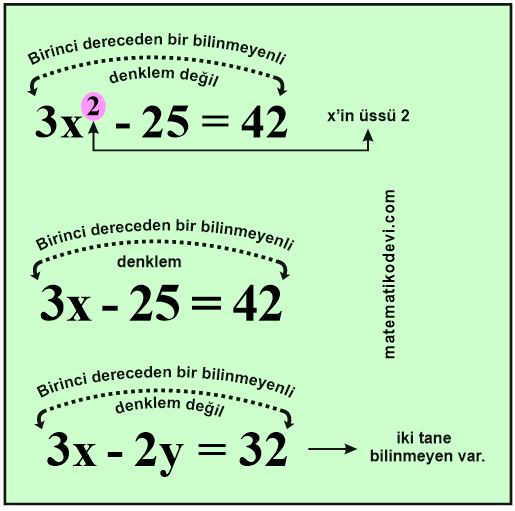
Örnek: 3x-7=21 eşitliği birinci dereceden bir bilinmeyenli denklemdir.
Örnek: katex is not defined – 8= 25 eşitliği birinci dereceden bir bilinmeyenli denklemdir.
📌 x’in katsayısı kesirli olabilir.
Örnek: x3 +8=20 eşitliği birinci dereceden bir bilinmeyenli denklem değildir.
📌 x2, x3, x4, x5, … gibi ifadelerden oluşan eşitlikler birinci dereceden olmadığı için birinci dereceden bir bilinmeyenli denklem değildir.
Örnek: katex is not defined -11=33 eşitliği birinci dereceden bir bilinmeyenli denklem değildir.
📌 Bilinmeyeni (x) kök içinde olan eşitlikler birinci dereceden olmadığı için birinci dereceden bir bilinmeyenli denklem değildir.
Bilgi:
✅ Bir denklemde değişkenin (x) denklemi sağlayan değerini bulma işlemine denklem çözmek denir.
✅ Değişkenin (x) denklemi sağlayan değerine denklemin kökü denir.
✅ Denklemin köklerinden oluşan kümeye çözüm kümesi denir ve çözüm kümesi Ç harfi ile gösterilir.
Örnek: 3x + 2 = 23 denklemini sağlayan tek bir x değeri vardır ve bu değer 3’tür.
✅ Denklem çözme (burada denklem çözme metotlarını kullanırız)
3x = 23 − 2
3x = 21
x=7
✅ Denklemin kökü = 7
✅ Çözüm kümesi: Ç = { 7 }
😲 Denklem kökünün küme biçiminde yazılması çözüm kümesi oluyor.
RASYONEL DENKLEMLER NASIL ÇÖZÜLÜR?
Rasyonel ifade şeklinde bulunan denklemleri çözerken kesirlerde yaptığımız gibi payda eşitleyebiliriz, genişletme veya sadeleştirme yapabiliriz, içler-dışlar çarpımı yapabiliriz. Şimdi bu denklem çözme yöntemlerini inceleyelim.
Bilgi: Rasyonel denklemleri çözerken ;
✅ Eşitliğin sağ ve sol tarafındaki rasyonel ifadelerin paydalarını eşitleriz.
✅ Paydalar eşitlendikten sonra paydaları silip payları birbirine eşitleniriz.
✅ Paylar eşitlendikten sonra 7.sınıfta öğrendiğimiz denklem çözme metotlarını kullanarak denklemi çözeriz.
Örnek: katex is not defined = katex is not defined rasyonel denklemi çözelim.
✅ Rasyonel denklemin paydalarını eşitleriz.
katex is not defined = katex is not defined
katex is not defined = katex is not defined
✅ Paydalar eşitlendikten sonra paydaları silip payları birbirine eşitleniriz.
3x-12=2x
✅ Denklem çözme metodu olan bilinenleri bir tarafa bilinmeyenleri bir tarafa toplarız.
3x-2x=12
x=12
✅ katex is not defined = katex is not defined denkleminin kökü 12’dir diyebiliriz.
Not: İşlemler sonunda bulduğumuz denklemdeki bilinmeyenin değerine denklemin kökü denir. Denklemin köklerinin oluşturduğu kümeye denklemin çözüm kümesi denir.
Örnek: katex is not defined + katex is not defined = katex is not defined rasyonel denklemi çözelim.
✅ Rasyonel denklemin paydalarını eşitleriz.
katex is not defined + katex is not defined = katex is not defined
katex is not defined + katex is not defined = katex is not defined
✅ Paydalar eşitlendikten sonra paydaları silip payları birbirine eşitleniriz.
6x+3+2x-8=x+9
8x-5=x+9
✅ Denklem çözme metodu olan bilinenleri bir tarafa bilinmeyenleri bir tarafa toplarız.
8x-5=x+9
8x-x=9+5
7x=14
x=2
✅ katex is not defined + katex is not defined = katex is not defined denkleminin kökü 2’dir diyebiliriz.
Örnek: katex is not defined – katex is not defined = katex is not defined rasyonel denklemi çözelim.
✅ Rasyonel denklemin paydalarını eşitleriz.
katex is not defined – katex is not defined = katex is not defined
katex is not defined – katex is not defined = katex is not defined
✅ Paydalar eşitlendikten sonra paydaları silip payları birbirine eşitleniriz.
8x-12-(5x-10)=2x+14
😲 aradaki eksi parantezin içindeki terimlerin işaretini tersine çevirir.❗
8x-12-5x+10=2x+14
3x-2=2x+14
✅ Denklem çözme metodu olan bilinenleri bir tarafa bilinmeyenleri bir tarafa toplarız.
3x-2=2x+14
3x-2x=14+2
x=16
✅ katex is not defined – katex is not defined = katex is not defined denkleminin kökü 16’dır diyebiliriz.
Bilgi: Rasyonel katsayılı denklemleri çözerken içler dışlar çarpımı yapabiliriz.
Örnek: katex is not defined = katex is not defined rasyonel denklemi çözelim.
✅ İçler Dışlar Çarpımı yapalım
3·(3x+7) = 2·x
9x+21 = 2x
✅ x’i yalnız bırakalım.
9x-2x=-21
7x=-21
x=-3
Yeni Nesil Soru
🎥 Bir Soru Bir Video 🎥
Soru: Dikdörtgen şeklindeki bir salonun zeminini genişliği 60 cm olan ve 20 cm olan halılarla şekilde verilen görseldeki gibi bir mavi halı bir sarı halı olacak şekilde sıra ile döşenecektir. Başlangıçta duvar ile halı arasında boşluk olmayıp son halı ile duvar arasında 20 cm boşluk bulunmaktadır.
Aynı salonu sarı renkli halıların genişliğini 10 cm kısaltıp mavi halıların sayısını 2 arttırılarak sıra ile döşenmiştir. Bu düzenlemede ilk duvar ile son duvar arasında hiç boşluk kalmayıp son halı mavi halı ile bitmiştir.
Buna göre başlangıçta kaç mavi halı kullanılmıştır?
| A) 11 cm | B) 12 cm | C) 13 cm | D) 14 cm |
Çözüm:
Konu Anlatımı Devamı : https://www.matematikodevi.com/koordinat-sistemi-konu-anlatimi/