Üçgende Kenarortay, Açıortay ve Yükseklik
Kazanım: Üçgende kenarortay, açıortay ve yüksekliği inşa eder.
Bu konuda neler öğreneceğiz :
Üçgende Kenarortay, Açıortay ve Yükseklik
Kenarortay:
Bilgi: Bir üçgenin herhangi bir kenarının orta noktasın ile aynı kenarının karşı köşe noktasını birleştiren doğru parçasına üçgenin o kenarına ait kenarortayı denir. Kenarortay “V” harfi ile gösterilir. Bir ABC üçgeninde;
✅ “a” kenarına ait kenarortay Va sembolü ile gösterilir.
✅ “b” kenarına ait kenarortay Vb sembolü ile gösterilir.
✅ “c” kenarına ait kenarortay Vc sembolü ile gösterilir.

✅ Yukarıda verilen DEF üçgeninde ;
[DK] doğru parçası [EF] kenarını iki eşit parçaya ayırmıştır. Bu yüzden [DK] kenarortaydır.
[FM] doğru parçası [DE] kenarını iki eşit parçaya ayırmıştır. Bu yüzden [FM] kenarortaydır.
[EL] doğru parçası [DF] kenarını iki eşit parçaya ayırmıştır. Bu yüzden [EL] kenarortaydır.
✅ Kenarortaylar üçgenin iç bölgesindeki bir noktada kesişmiştir.
✅ Tüm üçgenlerde kenarortayların kesişim noktası üçgenin iç bölgesindedir.
✅ Kenarortayların kesişim noktası olan bu noktaya Ağırlık Merkezi denir ve G harfiyle gösterilir.
Bilgi: Bir dik üçgende hipotenüse çizilen kenarortayın uzunluğu hipotenüs uzunluğunun yarısıdır. Bu kurala Muhteşem Üçlü Kuralı Özelliği denir.

✅ Yukarıda verilen KLM dik üçgeninde LN doğru parçası KM kenarını iki eşit parçaya ayırmıştır.
➡️ LN kenarortaydır.
✅ LN kenarortayı dik üçgende hipotenüse çizilmiştir.
➡️ LN kenarortayı KM kenarının yarısıdır.
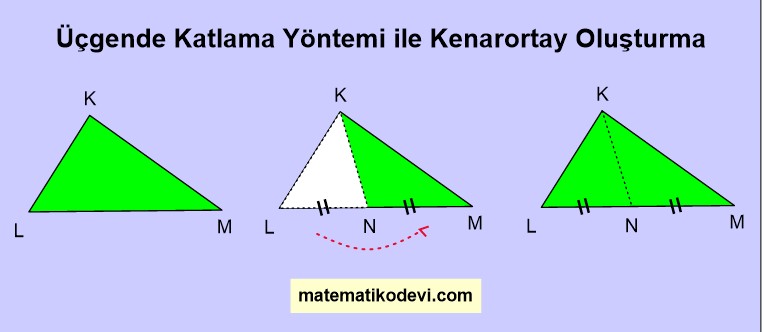
Üçgende Katlama Yöntemi ile Kenarortay Oluşturma
Açıortay:
Bilgi: Bir üçgenin herhangi bir iç açısını iki eş parçaya ayıran doğru parçasına üçgenin açıortayı denir. Açıortay “n” sembolü ile gösterilir. Bir ABC üçgeninde;
✅ “A” açısına ait açıortay na sembolü ile gösterilir.
✅ “B” açısına ait açıortay nb sembolü ile gösterilir.
✅ “C” açısına ait açıortay nc sembolü ile gösterilir.

✅ Yukarıda verilen ABC üçgeninde;
D açısının açıortayı [DC]
E açısının açıortayı [EB]
F açısının açıortayı [FA]
✅ Yukarıda verilen DEF üçgeninin açıortaylarının kesişim noktası üçgenin iç bölgesindedir.
✅ Tüm üçgenlerde açıortayların kesişim noktası üçgenin iç bölgesindedir.
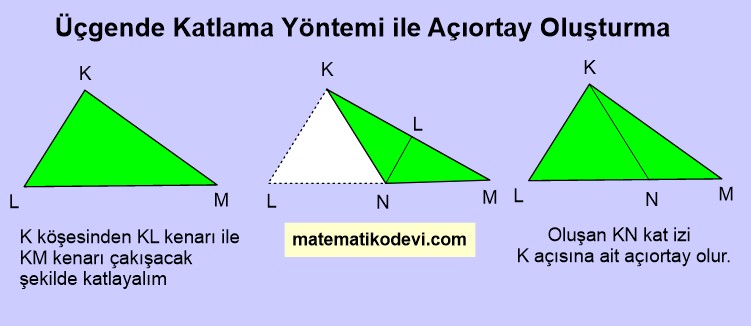
Üçgende Katlama Yöntemi ile Açıortay Oluşturma
Üçgende katlama yöntemi ile açıortay oluştururken üçgenin bir köşesine ait iki kenarı çakışacak şekilde katlarız. Oluşan kat izi açıortay olur.
Yükseklik:
Bilgi: Bir üçgenin bir köşesinden karşı kenarına veya uzantısına indirilen dik doğru parçasına üçgenin o kenarına ait yüksekliği denir. Yüksekliği “h” harfi ile gösteririz. Bir ABC üçgeninde;
✅ “a” kenarına ait yükseklik ha sembolü ile gösterilir.
✅ “b” kenarına ait yükseklik hb sembolü ile gösterilir.
✅ “c” kenarına ait yükseklik hc sembolü ile gösterilir.

Üçgenlerin Açı Çeşidine Göre Yükseklik Çizimi
Üçgenler açılarına göre dar, dik ve geniş açılı olma üzere üçe ayrılır.
Bilgi: Yükseklik çizimi üçgen çeşidine (dar açılı, dik açılı ve geniş açılı) göre farklılık göstermektedir. Bu yüksekliklerin üçgenin çeşidine göre nasıl farklılık gösterdiğini aşağıda verilen örneklerle inceleyelim.
Dar açılı üçgende yükseklik çizimi :

✅ Yukarıda resimde verilen dar açılı üçgende:
[KL] kenarına ait yükseklik [PM]
[LM] kenarına ait yükseklik [KS]
[KM] kenarına ait yükseklik [LR]’dir.
✅ Yukarıda resimde verilen dar açılı üçgende yüksekliklerin kesişim noktası O noktasıdır.
✅ O noktası üçgenin iç bölgesindedir.
✅ Dar açılı üçgenlerde yüksekliklerinin kesim noktası üçgenin iç bölgesindedir.
Dik açılı üçgende yükseklik çizimi :

✅ Yukarıda resimde verilen dik açılı üçgende:
[KL] kenarına ait yükseklik [LM]
[LM] kenarına ait yükseklik [KL]
[KM] kenarına ait yükseklik [LN]’dİr.
✅ Yukarıda resimde verilen dik açılı üçgende yüksekliklerin kesişim noktası L noktasıdır.
✅ L noktası üçgenin üzerindedir. (dik köşesinde)
✅ Dik açılı üçgenlerde yüksekliklerinin kesim noktası üçgenin üzerindedir.
Geniş açılı üçgende yükseklik çizimi :

✅ Yukarıda resimde verilen geniş açılı üçgende:
[EF] kenarına ait yükseklik [DB]
[DE] kenarına ait yükseklik [FC]
[DF] kenarına ait yükseklik [EA]’dır.
✅ [DB] ve [FC] yükseklikleri üçgenin dışında iken [EA] yüksekliği üçgenin içindedir.
✅ Yukarıdaki resimde gösterildiği gibi yüksekliklerin kesim noktası üçgenin dışındadır.
✅ Geniş açılı üçgenlerde yüksekliklerin kesim noktası üçgenin dışındadır.
Bilgi: Bir ikizkenar üçgende ikiz olmayan kenara ait yükseklik , aynı zamanda hem kenarortay hem de açıortaydır.

✅ Yukarıda verilen KLM üçgeninde |KL|=|KM| (ikizkenar üçgen)
✅ İkizkenar üçgende ikiz olmayan kenara (LM kenarına) yükseklik çizilmiş. (KN yükseklik)
✅ KN yüksekliği LM kenarını iki eşit parçaya böler.(KN kenarortaydır.)
✅ KN yüksekliği K açısını iki eşit parçaya böler.(KN açıortaydır.)
Üçgende Katlama Yöntemi ile Yükseklik Oluşturma
Bir üçgenin bir köşenden karşısındaki kenarı çakışacak şekilde katladığımızda oluşan kat izi yükseklik olur.

Bilgi: Bir eşkenar üçgende üçgenin kenarortayı , aynı zamanda açıortayı ve yüksekliğidir.

✅ Yukarıda verilen DEF üçgeninde DM,EL ve FK doğru parçaları ;
➡️ Hem açıortay
➡️Hem kenar ortay
➡️Hem de yükseklik doğrusudur.
Bilgi: Her hangi bir çeşitkenar üçgende kenar ortay(v) açıortay(n) ve yükseklik(h) elemanlarının uzunluk sıralaması;
Va>na>ha şeklindedir.
✅ Aşağıda verilen çeşitkenar üçgende çizilen kenar ortay(v) açıortay(n) ve yükseklik(h) elemanlarını inceleyiniz.

✅ Herhangi bir çeşitkenar üçgende aynı köşeye ait kenar ortay açıortay yükseklik elemanlarından en kısa olanı yükseklik, en uzun olanı ise kenarortaydır.
🎥 Bir Soru Bir Video 🎥
Soru:

Yukarıda verilen şekilde PRS bir üçgen ve |RT|=|TS| ‘dir.
PRS üçgeninin yüksekliklerinin kesim noktası P noktasıdır.
Buna göre RS uzununluğu kaç cm’dir?
Çözümü izle:

