Eğim ve Doğrunun Eğimi Konu Anlatımı
Bu konuda neler öğreneceğiz :
Eğim ve Doğrunun Eğimi
Kazanım: Doğrunun eğimini modellerle açıklar, doğrusal denklemleri ve grafiklerini eğimle ilişkilendirir.
EĞİM NEDİR?
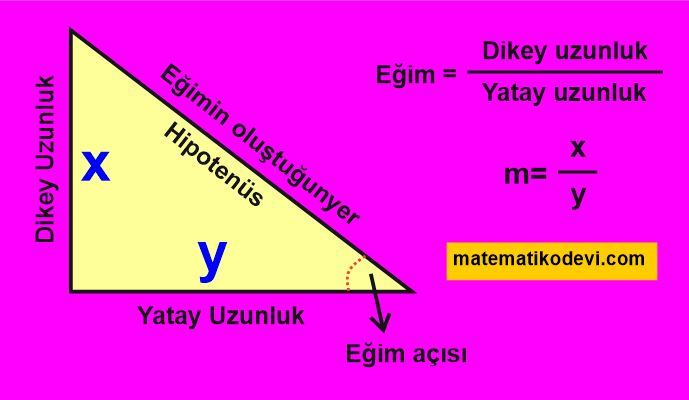
Bilgi: Dikey uzunluğun yatay uzunluğa oranına eğim denir ve “m” sembolü ile gösterilir.
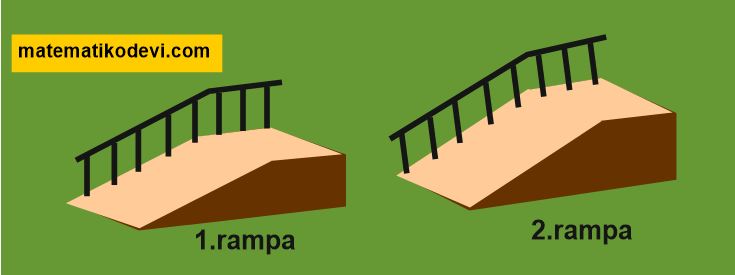
🤔 Sizce yukarıdaki rampalardan hangisine çıkarken daha çok zorlanırız?
😲 2.rampadan çıkarken 1.rampaya göre daha çok zorlanırız. Çünkü 2.rampanın eğimi 1.rampanın eğiminde daha fazladır.
Bir dik üçgende eğim (hipotenüs) dikey uzunluğun yatay uzunluğa bölünmesi ile hesaplanır. Eğimin olduğu uzunluk ile yatay uzunluğun arasında kalan açıya eğim açısı denir.
Örnek:
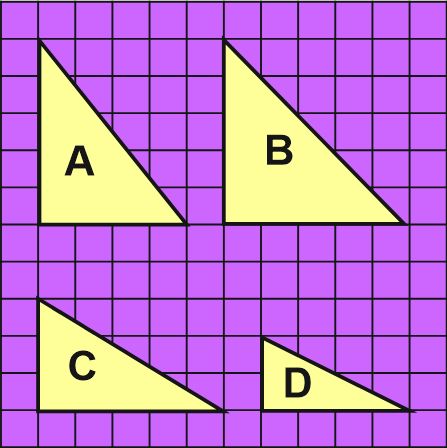
Yukarıda verilen A,B,C ve D rampalarının eğimini bulalım.
A rampasının eğimi 👇🏻
A rampasının dikey uzunluğu = 5 br
A rampasının yatay uzunluğu = 4 br
A rampasının eğimi = \dfrac{5}{4}
B rampasının eğimi 👇🏻
B rampasının dikey uzunluğu = 5 br
B rampasının yatay uzunluğu = 5 br
B rampasının eğimi = \dfrac{5}{5} =1
C rampasının eğimi 👇🏻
C rampasının dikey uzunluğu = 3 br
C rampasının yatay uzunluğu = 5 br
C rampasının eğimi = \dfrac{3}{5}
D rampasının eğimi 👇🏻
D rampasının dikey uzunluğu = 2 br
D rampasının yatay uzunluğu = 4 br
D rampasının eğimi = \dfrac{2}{4} = \dfrac{1}{2}
Not: Bir rampanın eğimi verilip dikey veya yatay uzunluklarından biri verilmediğinde verilmeyen uzunluğu bulmak için;
✅ Eğimi hesaplayıp verilen eğime eşitleriz ve içler dışlar çarpımı yapıp verilmeyen uzunluğu buluruz.
Örnek:
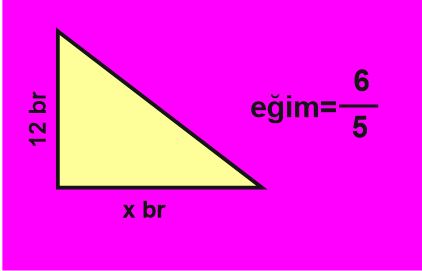
Yukarıda verilen rampanın yatay uzunluğunu bulalım.
rampanın eğimi = \dfrac{12}{x}
aynı rampanın eğimi \dfrac{6}{5} olarak verilmiş.
Bu iki ifade birbirine eşit olduğu için bu iki ifadeyi birbirine eşitleriz.
\dfrac{12}{x} = \dfrac{6}{5}
içler dışlar çarpımı yaparız.
12·5=6·x
60=6x
x=10 br rampanın yatay uzunluğu
Not: Eğimi ondalıklı kesir veya yüzde olarak ifade edebiliriz.
Örnek: \dfrac{7}{10} olarak verilen bir eğimi 0,7 veya %70 olarak da ifade edebiliriz.
DOĞRUNUN EĞİMİNİ HESAPLAMA
Bilgi: Bir doğrunun eğimi, doğru üzerinde bulunan iki nokta arasındaki dikey değişimin yatay değişime oranıdır.
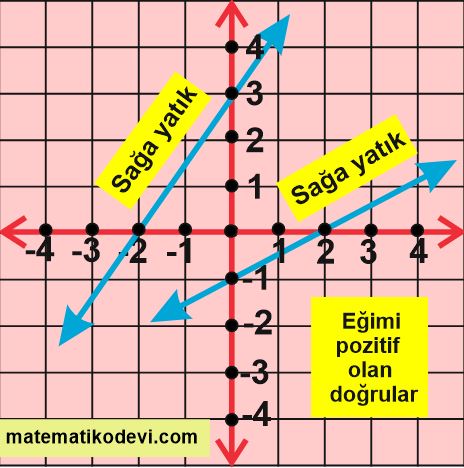
✅ Koordinat sisteminde y eksenine göre sağa yatık doğruların eğimi pozitiftir.
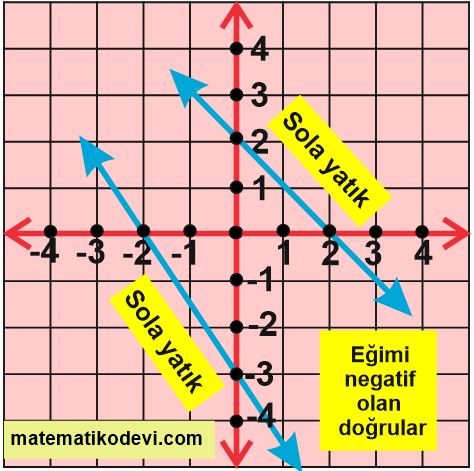
✅ Koordinat sisteminde y eksenine göre sola yatık doğruların eğimi negatiftir.
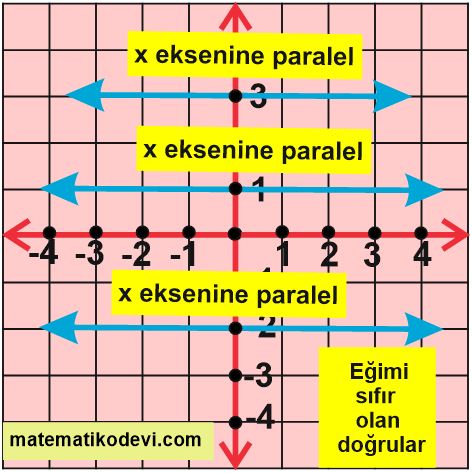
✅ Koordinat sisteminde x eksenine paralel olan doğruların eğimi sıfırdır.
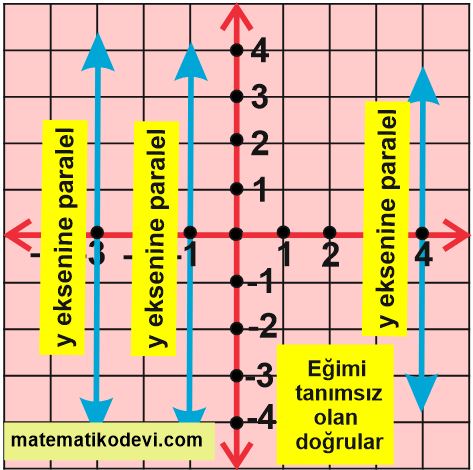
✅ Koordinat sisteminde y eksenine paralel olan doğruların eğimi tanımsızdır.
Aşağıda verilen görsellerde pozitif , negatif , sıfır ve tanımsız eğimlere örnek verilmiştir.
Bilgi: Koordinat sisteminde verilen doğrunun eğimini hesaplarken doğru hipotenüs olacak şekilde bir dik üçgen oluşturup oluşturduğumuz dik üçgen üzerinden doğrunun eğimini hesaplarız.
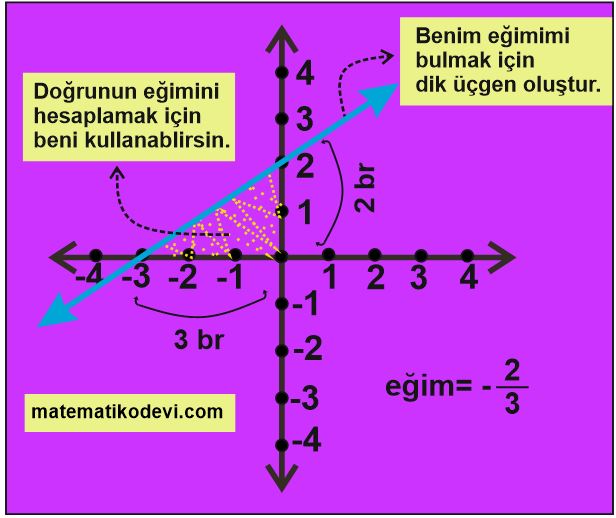
Aşağıdaki örnekleri inceleyerek doğrunun eğiminin nasıl hesaplandığını pekiştirelim.
Örnek: Aşağıda koordinat sisteminde verilen doğrunun eğimini bulalım.
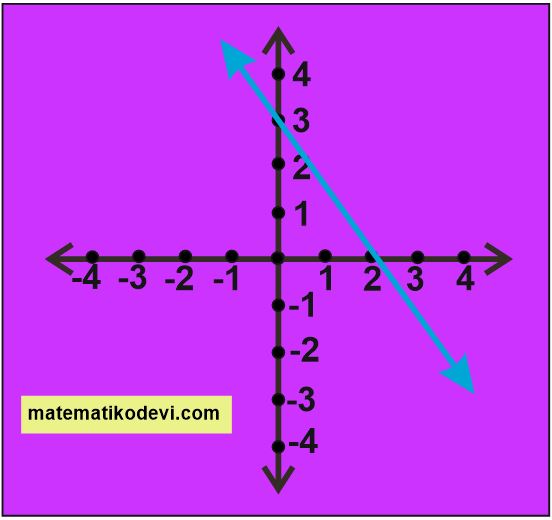
Çözüm:
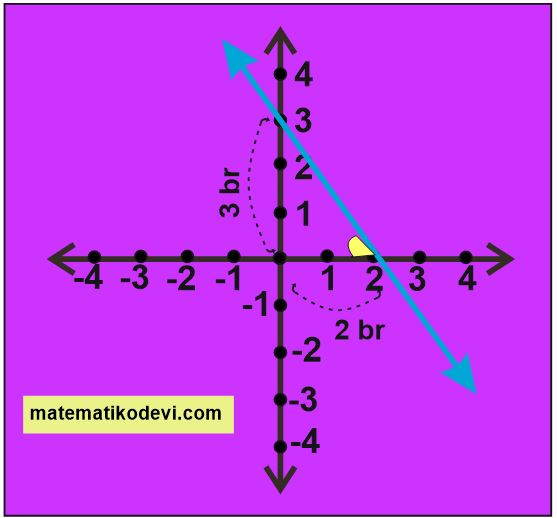
Yukarıdaki doğruyu incelediğimizde doğrunun koordinat sisteminde oluşturduğu dik üçgenin dikey uzunluğu 3 br , yatay uzunluğu 2 br ‘dir.
O zaman doğrunun eğimi 👉 \dfrac{3}{2}
Örnek: Aşağıda koordinat sisteminde verilen doğrunun eğimini bulalım.
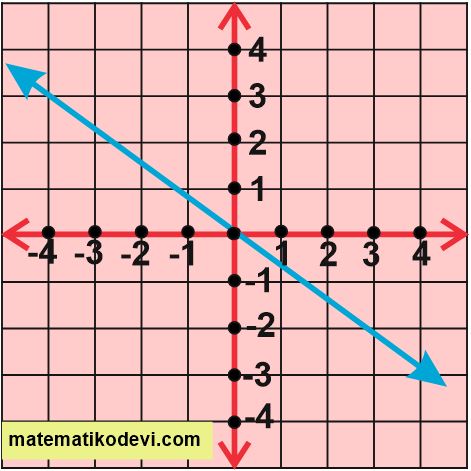
Çözüm: Yukarıda verilen doğrunun eğimini hesaplayabilmek için doğru hipotenüs olacak şekilde kenarları sayılabilecek bir dik üçgen oluşturmalıyız.
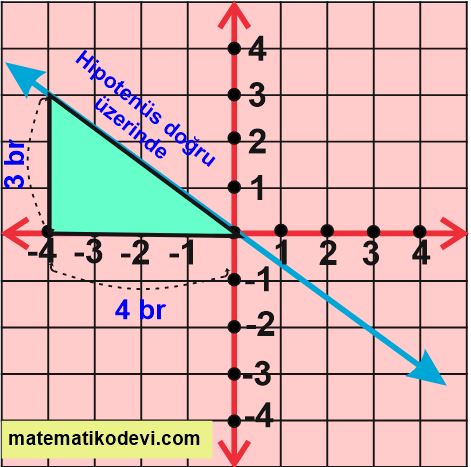
Yukarıdaki doğruyu incelediğimizde doğrunun koordinat sisteminde oluşturduğu dik üçgenin dikey uzunluğu 3 br , yatay uzunluğu 4 br ‘dir.
O zaman doğrunun eğimi 👉 \dfrac{3}{4}
Doğru sola yatık olduğu için eğimi negatif olur 👉 – \dfrac{3}{4}
Bilgi: Bir doğrunun koordinat sistemi üzerinde x ekseni ile yaptığı açılardan sağda olanına eğim açısı denir.
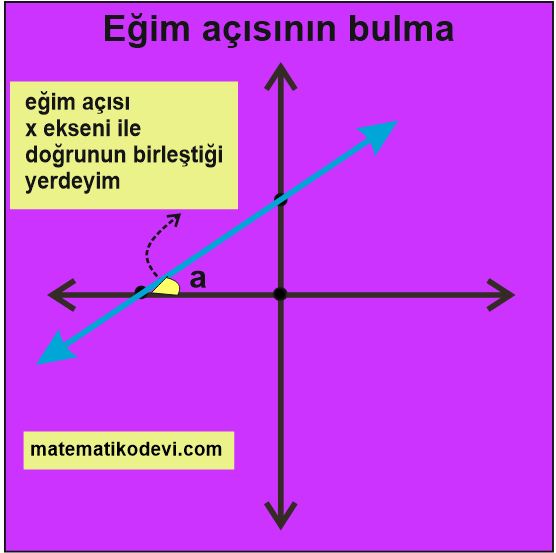
DENKLEMİ VERİLEN DOĞRUNUN EĞİMİNİ BULMA
Bilgi: Denklemi y=mx+n şeklinde verilen doğrularda x’in katsayısı doğrunun eğimidir.
👉 y=5x+3 denkleminin eğimi x ‘in katsayısı olan 5 ‘dir.
Örnek: Aşağıda denklemi verilen doğruların eğimini hesaplayalım.
➡ y= -2x +7 denkleminin eğimi ⤵
🤓 y= 6x +8 denkleminde x ‘in katsayısı -2 olduğu için denklemin eğimi -2 ‘dir.
➡ y= 6x +8 denkleminin eğimi ⤵
🤓 y= 6x +8 denkleminde x ‘in katsayısı 6 olduğu için denklemin eğimi 6 ‘dır.
➡ y= -8x -11 denkleminin eğimi ⤵
🤓 y= -8x -11 denkleminde x ‘in katsayısı -8 olduğu için denklemin eğimi -8 ‘dir.
Not: Bir denklemin eğimini hesaplarken y’nin katsayısı 1 değil ise ;
✅ Eşitliğin bir tarafında y terimi , eşitliğin diğer tarafında geriye kalan terimler olacak şekilde düzenlenir.
✅ Sonra eşitliğin her iki tarafı y ‘nin katsayısına bölünür.
✅ x’in katsayısı verilen denklemin eğimi olur.
Şimdi aşağıdaki örnekleri inceleyerek y’nin katsayısı 1 olmayan denklemlerin eğimlerinin nasıl hesaplanacağını pekiştirelim.
Örnek: 3y -4x+12=0 denkleminin eğimini bulalım.
✅ Eşitliğin bir tarafında y terimi , eşitliğin diğer tarafında geriye kalan terimler olacak şekilde düzenlenir.
3y -4x+12=0 🤓-4x ve 12 eşitliğin sol tarafına geçecek.
3y=4x-12 🤓 -4x ve 12 eşitliğin sol tarafına geçerken işaretini değiştirir.
✅ Sonra eşitliğin her iki tarafı y ‘nin katsayısına bölünür.
3y=4x-12 🤓 y’nin katsayısı 3 olduğu için her iki tarafı 3’e böleriz.
\dfrac{3y}{3} = \dfrac{4x}{3} – \dfrac{12}{3}
✅ x’in katsayısı verilen denklemin eğimi olur.
y= \dfrac{4x}{3} -4
x’in katsayısı \dfrac{4}{3}
3y -4x+12=0 denkleminin eğimi \dfrac{4}{3}
Örnek: 5y + 6x +20=0 denkleminin eğimini bulalım.
✅ Eşitliğin bir tarafında y terimi , eşitliğin diğer tarafında geriye kalan terimler olacak şekilde düzenlenir.
5y + 6x +20=0 🤓 6x ve 20 eşitliğin sol tarafına geçecek.
5y=-6x-20 🤓 6x ve 20 eşitliğin sol tarafına geçerken işaretini değiştirir.
✅ Sonra eşitliğin her iki tarafı y ‘nin katsayısına bölünür.
5y=-6x-20 🤓 y’nin katsayısı 5 olduğu için her iki tarafı 5’e böleriz.
\dfrac{5y}{5} = \dfrac{-6x}{5} – \dfrac{-20}{5}
✅ x’in katsayısı verilen denklemin eğimi olur.
y= -\dfrac{6x}{5} -4
x’in katsayısı -\dfrac{6}{5}
5y + 6x +20=0 denkleminin eğimi -\dfrac{6}{5}
İKİ NOKTASI BELLİ OLAN DOĞRUNUN EĞİMİNİ HESAPLAMA
Bilgi: Üzerindeki iki noktanın koordinatları belli olan doğrunun eğimini hesaplarken y eksenlerinin farkını x eksenlerinin farkına böleriz.

Örnek: A(2,6) ve B(4,10) noktalarından geçen doğrunun eğimini bulalım.
👉 y eksenlerin farkını bulalım.
10-6 🤓 ikinci sıradaki y ekseninden birinci sıradaki y eksenini çıkarırız.
4
👉 x eksenlerinin farkını bulalım.
4-2 🤓 ikinci sıradaki x ekseninden birinci sıradaki x eksenini çıkarırız.
2
👉 y eksenlerinin farkını , x eksenlerinin farkına bölelim.
\dfrac{4}{2}2
Örnek: K(-3,-5) ve L(-2,7) noktalarından geçen doğrunun eğimini bulalım.
👉 y eksenlerin farkını bulalım.
7-(-5) 🤓 ikinci sıradaki y ekseninden birinci sıradaki y eksenini çıkarırız.
7+5 🤓 arda arda eksi artıya dönüşür.
12
👉 x eksenlerinin farkını bulalım.
(-2)-(-3) 🤓 ikinci sıradaki x ekseninden birinci sıradaki x eksenini çıkarırız.
-2+3
1
👉 y eksenlerinin farkını , x eksenlerinin farkına bölelim.
\dfrac{12}{1}💨 K ve L noktalarından geçen doğrunun eğimi 12’dir.
Eğim Ve Doğrunun Eğimi Test
Eğim Ve Doğrunun Eğimi Konu Anlatımını tamamladıysanız aşağıdaki testi çözerek konuyu pekiştirebilirsiniz. Test açılmadıysa sayfayı yenileyiniz.
Yeni Nesil Soru
🎥 Bir Soru Bir Video 🎥
Soru:
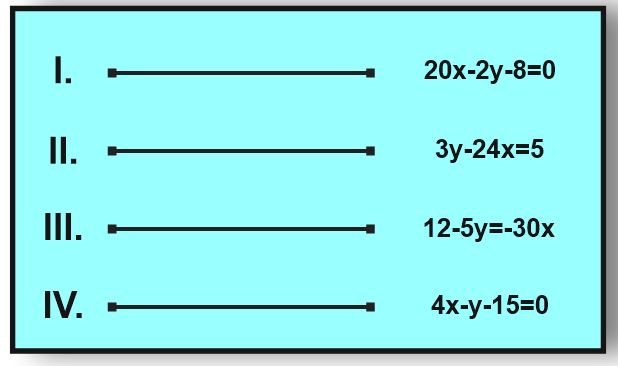
Yukarıda verilen eşit uzunluktaki demir çubuklar karşısında yazan denklemin eğimine göre aşağıdaki gibi A,B,C ve D rampaları oluşturuluyor.
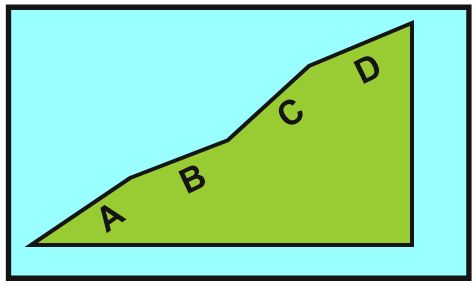
Bu rampayı tırmanan bisiklet sürücüsünün nabız atış grafiği aşağıdaki gibidir.
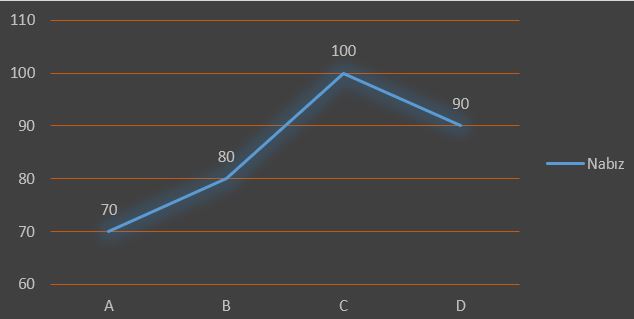
Buna göre A,B,C ve D rampası I,II,III ve IV ile gösterilen çubuklardan hangisine aittir?
| A) | A-I | B-II | C-III | D-IV |
| B) | A-III | B-I | C-II | D-IV |
| C) | A-IV | B-III | C-I | D-II |
| D) | A-III | B-II | C-IV | D-I |
Çözüm:

