Cebirsel İfadeleri Çarpanlara Ayırma Konu Anlatımı-8.Sınıf
Kazanım: Cebirsel ifadeleri çarpanlara ayırır.
Bu konuda neler öğreneceğiz :
Cebirsel İfadeleri Çarpanlara Ayırma
Bir cebirsel ifadeyi çarpanlarının çarpımı şeklinde yazmaya, o cebirsel ifadeyi çarpanlara ayırma denir. Cebirsel ifadeler çarpanlara ayrılırken farklı yöntemlerden faydalanılır. Aşağıda Cebirsel İfadeleri Çarpanlara Ayırma yöntemlerini tek tek inceleyelim.
1) Ortak Çarpan Parantezine Alma:
Ortak çarpan parantezine alma konusunu 6.sınıfta görmüştük.8.sınıfta farklı olarak ortak ifadeler çarpım şeklinde verilmeyecek biz ortak çarpanları bulup çarpım şeklinde yazacağız.Ortak çarpan parantezine alırken bulduğumuz ortak çarpanları parantezin dışına ve geriye kalan ortak olmayan terimleri parantezin içine yazarız.

Örnek: a2 + 4a cebirsel ifadesini ortak çarpan parantezine alma yöntemi ile çarpanlarına ayıralım.
➡ Terimleri çarpım şeklinde yazalım.
a·a +3·a
➡ Ortak olan ifadeleri kırmızı renk ile gösterelim.
a·a +3·a
➡ Ortak olan terimi parantez dışında , geriye kalan terimleri parantez içinde yazalım.
a·(a +3)
Örnek: 8x2 -2x cebirsel ifadesini ortak çarpan parantezine alma yöntemi ile çarpanlarına ayıralım.
➡ Terimleri çarpım şeklinde yazalım.
2·4·x·x -2·x
➡ Ortak olan ifadeleri kırmızı renk ile gösterelim.
2·4·x·x –2·x
➡ Ortak olan terimi parantez dışında , geriye kalan terimleri parantez içinde yazalım.
2x·(4x – 1) 🤓 2x ‘in hepsi parantez dışına yazılırsa parantez içinde 1 kalır.
Örnek: 12x3 -15x2 cebirsel ifadesini ortak çarpan parantezine alma yöntemi ile çarpanlarına ayıralım.
➡ Terimleri çarpım şeklinde yazalım.
3·4·x·x·x – 3·5·x·x
➡ Ortak olan ifadeleri kırmızı renk ile gösterelim.
3·4·x·x·x – 3·5·x·x
➡ Ortak olan terimi parantez dışında , geriye kalan terimleri parantez içinde yazalım.
3x2·(4x – 5)
Ortak Çarpan Parantezine Alma Modelleme
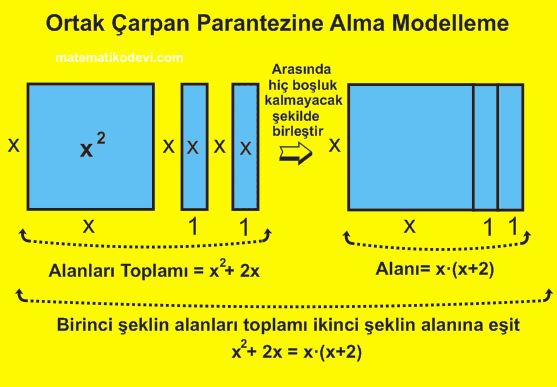
2) Gruplandırarak Çarpanlara Ayırma:
Bu yöntemde terimler kendi aralarında ortak çarpan bulunacak şekilde iki veya daha fazla gruplara ayrılır. Daha sonra ortak çarpan parantezine alınır. Gruplandırarak çarpanlara ayırma üçten fazla terimi olan cebirsel ifadelerde kullanılır. Gruplandırma metodunda gruplara ayırdıktan sonra parantez içindeki ifadeler aynı olması gerekir.
Örnek: xy + yz + xz + z2 cebirsel ifadesini gruplandırarak çarpanlarına ayıralım.
➡ Cebirsel ifadeyi gruplara ayıralım.
1.grup xy+xz
2.grup yz+ z2 olsun
➡ Ayırdığımız grupları ortak çarpan parantezine ayıralım.
1.grup xy+xz ➯ x(y+z)
2.grup yz+ z2 ➯ z(y+z)
Dikkat edersek 1. ve 2. grubun parantez içleri aynı
➡ Gruplandırarak ortak çarpan parantezine aldıktan sonra x(y+z)+z(y+z) parantez içleri aynı olduğu için çarpanlardan biri parantez içi olacak şekilde ortak çarpan paranteze alalım.
(y+z)(x+z)
Not: Gruplara ayırırken parantez içleri aynı olacak şekilde gruplara ayırmamız lazım.
Örnek: by + 2ax + 2bx + ay cebirsel ifadesini gruplandırarak çarpanlarına ayıralım.
➡ Cebirsel ifadeyi gruplara ayıralım.
1.grup by+2bx
2.grup 2ax+ ay olsun
➡ Ayırdığımız grupları ortak çarpan parantezine ayıralım.
1.grup by+2bx ➯ b(y+2x)
2.grup 2ax+ ay ➯ a(2x+y)
Dikkat edersek 1. ve 2. grubun parantez içleri aynı
➡ Gruplandırarak ortak çarpan parantezine aldıktan sonra b(y+2x) + a(2x+y) parantez içleri aynı olduğu için çarpanlardan biri parantez içi olacak şekilde ortak çarpan paranteze alalım.
(y+2x)(a+b)
3) Özdeşliklerden Yararlanarak Çarpanlara Ayırma:
Özdeşlikleri kullanarak çarpanlara ayırmada iki kare farkı özdeşliği ve tam kare özdeşliğinden yararlanarak çarpanlara ayıracağız. Şimdi bu özdeşlikleri kullanarak çarpanlara ayırma yöntemini inceleyelim
A)Tam Kare Özdeşliği ile Çarpanlara Ayırma:
Özdeşlikler konusunda öğrendiğimiz tam kare özdeşliğini bazı cebirsel ifadeleri çarpanlara ayırmada kullanabiliriz.
Bu yöntemde cebirsel ifade 3 terimden oluşur. Terimlerden 2 tanesi bir terimin karesi olacak ve 3.terimde karesi olan terimlerin çarpımının 2 katı olmalı. Bu şekilde olan cebirsel ifadeleri terimlerin toplamının parantez karesi şeklinde yazabiliriz.
Bilgi: İki terimin toplamının karesi, bu iki terimin kareleri ile bu iki terimin çarpımının iki katının toplamına eşittir.
✅ (x + y)2 = x2 + 2xy + y2
İki terimin farkının karesi, bu iki terimin kareleri toplamından bu iki terimin çarpımının iki katının çıkarılmasına eşittir.
✅ (x − y)2 = x2 − 2xy + y2

Örnek: (4a-5b)2 ifadesinin eşitini tam kare özdeşliğinden yararlanarak bulalım.
➡ Birinci terimin karesi
(4a)2 = 16a2
➡ İkinci terimin karesi
(5b)2 = 25b2
➡ Birinci terim ile ikinci terimin çarpımının iki katı
2· 4a·5b=40ab
➡ Birinci terim ile ikinci terimin karelerinin toplamından birinci terim ile ikinci terimin çarpımının iki katının çıkarılması
16a2 + 25b2 – 40ab
16a2 – 40ab + 25b2
Örnek: (2x+3y)2 ifadesinin eşitini tam kare özdeşliğinden yararlanarak bulalım.
➡ Birinci terimin karesi
(2x)2 = 4x2
➡ İkinci terimin karesi
(3y)2 = 9y2
➡ Birinci terim ile ikinci terimin çarpımının iki katı
2·2x·3y=12xy
➡ İki terimin kareleri ile bu iki terimin çarpımının iki katının toplamına eşittir.
4x2 + 9y2 + 12xy
16a2 + 20ab + 25b2
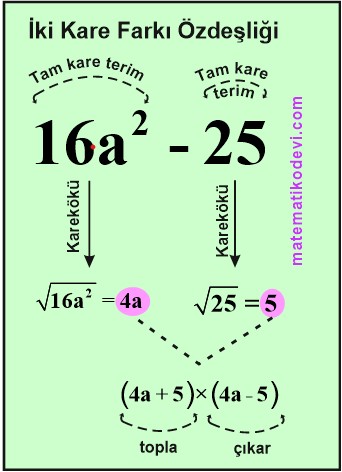
B) İki Kare Farkı Özdeşliği ile Çarpanlara Ayırma:
Özdeşlikler konusunda öğrendiğimiz iki kare farkı özdeşliğini bazı cebirsel ifadeleri çarpanlara ayırmada kullanabiliriz.
Bu yöntemde cebirsel ifade 2 terimden oluşur. Cebirsel ifadedeki bu 2 terim de tam kare terim olmalı ve birbirinden çıkarılmalı. Bu şekildeki cebirsel ifadeleri bu iki terimin kareköklerinin toplamı ile farkının çarpımı şeklinde yazabiliriz.
Örnek: 9x2-36b2 ifadesinin eşitini iki kare farkı özdeşliğinden yararlanarak bulalım.
➡ Birinci terimin karekökü 🤓
\sqrt {9x^2} = 3x
➡ İkinci terimin karekökü 🤓
\sqrt {36b^2} = 6b
➡ İki terimin kareköklerinin toplamı ile farkının çarpımı 🤓
(3x+6b)·(3x-6b)
📌 9x2-36b2 ifadesi (3x+6b)·(3x-6b) ifadesinin özdeşi olduğu için birbirine eşittir.
Örnek: 49m4-4n6 ifadesinin eşitini iki kare farkı özdeşliğinden yararlanarak bulalım.
➡ Birinci terimin karekökü 🤓
\sqrt {49m^4} = 7m2
➡ İkinci terimin karekökü 🤓
\sqrt {4n^6} = 2n3
➡ İki terimin kareköklerinin toplamı ile farkının çarpımı 🤓
(7m2+2n3)·(7m2-2n3)
📌 49m4-4n6 ifadesi (7m2+2n3)·(7m2-2n3) ifadesinin özdeşi olduğu için birbirine eşittir.
Yeni Nesil Soru
🎥 Bir Soru Bir Video 🎥
Soru: Bilgi: Yol = Hız x Zaman ve x2-y2 = (x+y)·(x-y) olmak üzere;
Enes aralarındaki mesafe (80a2-45) km olan A şehrinden B şehrine saatte (4a-3) km sabit hızla gitmiştir. Enes B şehrinden dönerken hızını saatte 6 km arttırarak sabit hızla dönmüştür.
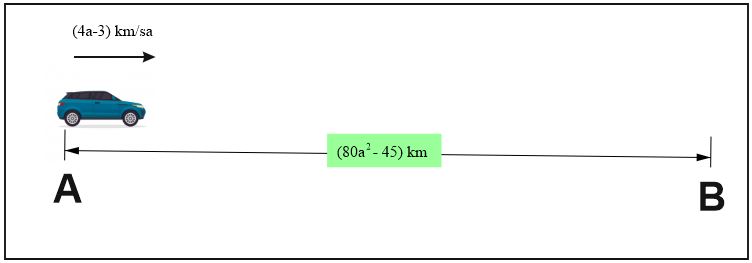
Buna göre Enes’in A şehrinden B şehrine gidiş ve dönüş süresi toplam kaç saattir?
| A) 40a-50 | B) 40a | C) 50 | D) 40a+50 |
Çözüm:
Cebirsel İfadeler Konu anlatımı bitti.
Konu ile alakalı test ve etkinlikler ile Cebirsel İfadeler konusunu pekiştirebilirsiniz.

