Basit Olayların Olma Olasılığını Hesaplama Konu Anlatımı
Kazanım: Basit bir olayın olma olasılığını hesaplar.
Basit Olayların Olma Olasılığını Hesaplama Konu Anlatımı aşağıda anlatılmıştır. Konuyu öğrendikten sonra yeni nesil sorumuzu çözmeyi unutmayın. 🤓
Bu konuda neler öğreneceğiz :
Basit Olayların Olma Olasılığını Hesaplama
Bilgi: Bir olasılık deneyinde çıktıların şansları birbirine eşit ise bu olasılık deneyinde bir olayın olma olasılığı; istenen olayın çıktılarının sayısının tüm çıktıların sayısına bölünmesiyle bulunur.
Bir olayın olma olasılığı = \dfrac{İstenen\ olayın \ çıktı \ sayısı}{Tüm \ olayın \ çıktı \ sayısı}
Örnek:

Yukarıda verilen eşit büyüklükteki toplar bir torba içine konulup içinden rastgele bir top çekiliyor.
Buna göre çekilen topun tek sayı olma olasılığını bulalım.
➡ Deney: Torbadan topun çekilmesi
➡ İstenen olay: Sayıların tek olması
➡ İstenen olayın çıktıları : 1,3,5,7,9 ( 5 tane )
➡ Tüm olayın çıktıları: 1,2,3,4,5,6,7,8,9 ( 9 tane )
➡ İstenen olayın olma olasılığı : \dfrac{5}{9}
Örnek:

4 kız ,5 erkeğin olduğu bir sınıftan rastgele bir öğrenci seçiyor.
Buna göre seçilen öğrencinin kız olma olasılığını bulalım.
➡ Deney: Bir öğrencinin seçilmesi
➡ İstenen olay: Seçilen öğrencinin kız olması
➡ İstenen olayın çıktıları : 1.kız,2.kız,3.kız,4.kız ( 4 tane )
➡ Tüm olayın çıktıları: 1.kız,2.kız,3.kız,4.kız, 1.erkek,2.erkek,3.erkek,4.erkek,5.erkek( 9 tane )
➡ İstenen olayın olma olasılığı : \dfrac{4}{9}
Not: Bir olayın olma olasılığını kesirli olarak, yüzde olarak veya ondalıklı olarak ifade edebiliriz.
Örneğin Bir madeni para havaya atıldığında tura gelme olasılığı \dfrac{1}{2} ‘dir.
Bu olasılığı yüzde olarak %50 ondalıklı kesir olarak 0,5 şeklinde ifade edebiliriz.
Bilgi: Bir olayın olma olasılığı ile olmama olasılığı toplamı 1’dir.Yani 1 olayın olmama olasılığını bulmak için 1’den bir olayın olma olasılığını çıkarırız.

Örnek:
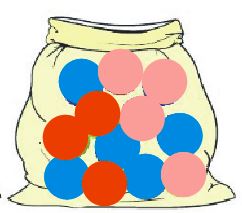
Yukarıda verilen eşit büyüklükteki toplar içinden rastgele bir top çekiliyor.
Buna göre çekilen topun kırmızı olmama olasılığını bulalım.
➡ 1’den kırmızı gelme olasılığını çıkarırsak kırmızı gelmeme olasılığını buluruz.
➡ Deney: Torbadan topun çekilmesi
➡ İstenen olay: kırmızı gelmesi
➡ İstenen olayın çıktıları : 1.kırmızı,2.kırmızı,3,kırmızı ( 3 tane )
➡ Tüm olayın çıktıları: 1.kırmızı,2.kırmızı,3,kırmızı,1.Pembe,2.pembe,3.pembe,4.pembe,1.mavi,2.mavi,3.mavi,4.mavi,5.mavi ( 12 tane )
➡ İstenen olayın olma olasılığı : \dfrac{3}{12}
➡ Kırmızı gelmeme olasılığı: 1- \dfrac{3}{12} = \dfrac{9}{12}
Bilgi: Bir olasılık sorusunda iki olay veya ile bağlanmış ise bu iki olayın olasılıkları toplanır.
Örnek:

Yukarıda verilen kartlar üzerine ‘MATEMATİK’ kelimesi yazılıp bir torbaya atılıyor.
Buna göre torbadan çekilen kartın ”A” veya ”E” olma olasılığını bulalım.
➡ Deney: Torbadan kartın çekilmesi
➡ İstenen olay: A gelmesi
➡ İstenen olayın olma olasılığı : \dfrac{2}{9}
➡ İstenen olay: E gelmesi
➡ İstenen olayın olma olasılığı : \dfrac{1}{9}
➡ İstenen olay: A veya E gelmesi
➡ İstenen olayın olma olasılığı : \dfrac{2}{9} + \dfrac{1}{9} = \dfrac{3}{9}
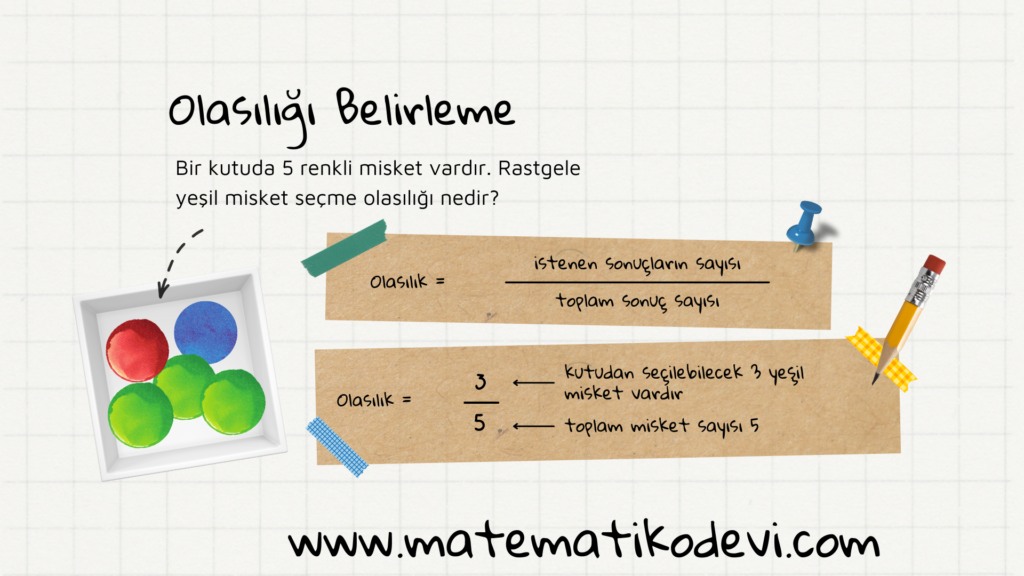
Olasılık Afiş:
Aşağıda olasılık konusunu özetleyen afişleri inceleyip tekrar amaçlı kullanabilirsiniz.






Olasılık Test 8.Sınıf
Yeni Nesil Soru
🎥 Bir Soru Bir Video 🎥
Soru: Aşağıda verilen labirentte ok yönünde ilerleyen köpek kulübeye ulaşmaya çalışmaktadır.
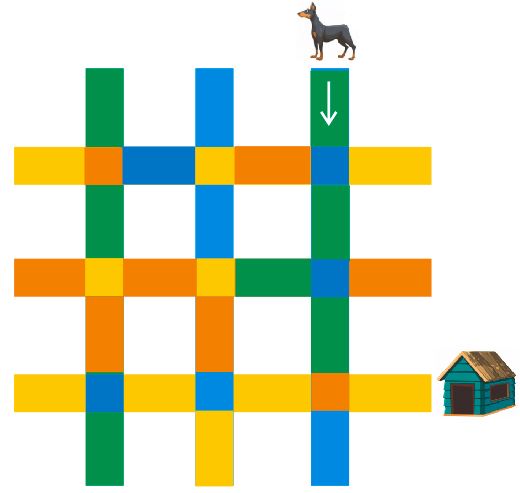
Köpek yol ayrımına geldiğinde aşağıdaki gibi hareket etmektedir.
- Seçeneklerin hepsi aynı renkte ise sağa doğru hareket etmektedir.
- Seçeneklerden ikisi aynı ise aynı olan renklerden birini seçmektedir.
- Seçeneklerden hepsi farklı ise aynı doğrultuda hareket etmektedir.
Buna yukarıdaki şartlara göre hareket eden köpek kulübesine ulaşma olasılığı kaçtır?
A) \dfrac{1}{2} \qquad B) \dfrac{1}{3}\qquad C) \dfrac{1}{4}\qquad D) \dfrac{1}{5}
Çözüm:

